One-way ANOVA (Lab 9)

Learn to use the most basic kind of ANOVA in Jamovi
labs
jamovi
tests
anova
Author
Affiliation

Justin Dainer-Best

Bard College

Published

April 4, 2024

Objectives

Today’s lab’s objectives are to:

  • Learn about one-way ANOVAs
  • Learn how to conduct a one-way ANOVA by calculating \(MS_{within}\) and \(MS_{between}\)
  • And then learn how to calculate an ANOVA, easily and efficiently, Jamovi
  • Visualize the results of ANOVAs

You’ll turn in an “answer sheet” on Brightspace. Please turn that in by the end of the weekend.

Analysis of Variance (ANOVA)

In an ANOVA, we are comparing two or more independent groups on an interval or ratio variable—our independent variable (IV) is categorical (e.g., group membership / treatment group), and our dependent variable (DV) is numeric.

In a one-way ANOVA, most of the time, we want to test whether or not there is an effect of group (with more than two levels) on some dependent variable. We’ll be using open data from Experiment 2 from James et al. (2015).

James, E. L., Bonsall, M. B., Hoppitt, L., Tunbridge, E. M., Geddes, J. R., Milton, A. L., & Holmes, E. A. (2015). Computer game play reduces intrusive memories of experimental trauma via reconsolidation-update mechanisms. Psychological Science, 26, 1201–1215. https://doi.org/10.1177%2F0956797615583071

The experiment

James and colleagues were interested in the experiences of having flashbacks (intrusive memories of traumatic experiences). Past research has found that simply “trying to forget” doesn’t work well—but we can change memories while we’re remembering them. Importantly, research also shows that during reconsolidation, traumatic memories can be altered and weakened to the point that they are no longer intrusive. The researchers knew that these flashbacks are often visual, and so they decided to interrupt them with a visual task—the puzzle video game Tetris.

So they asked: does playing Tetric while a memory is being reconsolidated interfere with the storage of it? Does that make the memory less likely to reoccur? They hypothesized that only participants who played Tetris after reactivation of the traumatic memories would experience a reduction in intrusive memories. In comparison, simply playing the game (without reactivation to trigger reconsolidation) or reactivation of the memory (without Tetris), would not reduce the occurrence intrusive memories.

To test their hypothesis, the authors conducted an experiment (total N = 72; n = 18 per condition; across four conditions). All participants viewed a series of video clips of graphic violence (e.g., a person getting hit by a van while using his phone as he crossed the road) as a way to create memories that should become intrusive memories. Participants then went home and recorded the number of intrusive memories they experienced over the next 24 hours.

Before any experimental manipulations, all groups were predicted to have an equal occurrence of intrusive memories during the first 24 hours (called Day 0).

After the first 24-hour period, the participants returned to the lab and completed the experiment. Participants were randomly assigned to ONE of the conditions described below.

Download the data from Brightspace or here.

The conditions

  1. No-task control: These participants completed a 10-minute music filler task.

  2. Reactivation + Tetris: These participants were shown a series of images from the trauma film to reactivate the traumatic memories (i.e., reactivation). After a 10-minute music filler task, participants played Tetris for 12 minutes.

  3. Tetris Only: These participants played Tetris for 12 minutes, but did not complete the reactivation task.

  4. Reactivation Only: These participants completed the reactivation task, but did not play Tetris.

All participants were asked to record the number of intrusive memories that they experienced over the next seven days (Days 1 to 7). After the seven days had passed, participants completed an “Intrusion-Provocation” Task, in which they were shown blurred images from the trauma film and asked to indicate whether the blurred image triggered an intrusive memory.

The researchers hypothesized that the second condition (Reactivation + Tetris) would have the lowest number of intrusive memories in those seven days, and also that they would have the lowest scores on the Intrusion-Provocation Task.

Read the question below, and decide what you think before clicking for the answer.

Research hypothesis: NOT (People who are in the Reactivation+Tetris condition = those in the Reactivation condition = those in the Tetris-only condition = those in the control condition)

Null hypothesis: People who are in the Reactivation+Tetris condition = those in the Reactivation condition = those in the Tetris-only condition = those in the control condition

Remember, while the null is that these conditions are equivalent, the research hypothesis is simply that they’re not all equivalent.

Writing the following is incorrect for the research hypothesis—because it’s not necessarily the case that NONE are equal if the ANOVA finds significant results:

People who are in the Reactivation+Tetris condition \(\neq\) those in the Reactivation condition \(\neq\) those in the Tetris-only condition \(\neq\) those in the control condition

Explore the data

Scroll through the data briefly (up and down or right-to-left). You’ll notice lots of data, and some NAs. When you load the data into Jamovi you’ll see that Jamovi makes those NAs into blanks.

Condition Time_of_Day BDI_II STAI_T pre_film_VAS_Sad pre_film_VAS_Hopeless pre_film_VAS_Depressed pre_film_VAS_Fear pre_film_VAS_Horror pre_film_VAS_Anxious post_film_VAS_Sad post_film_VAS_Hopeless post_film_VAS_Depressed post_film_VAS_Fear post_film_VAS_Horror post_film_VAS_Anxious Attention_Paid_to_Film Post_film_Distress Day_Zero_Number_of_Intrusions Days_One_to_Seven_Number_of_Intrusions Visual_Recognition_Memory_Test Verbal_Recognition_Memory_Test Number_of_Provocation_Task_Intrusions Diary_Compliance IES_R_Intrusion_subscale Tetris_Total_Score Self_Rated_Tetris_Performance Tetris_Demand_Rating
1 2 1 33 0.0 0.0 0.0 0.4 0.3 0.8 1.0 0.3 0.0 0.3 0.6 1.2 9 8 2 4 15 18 5 9 0.62 NA NA 0
1 2 3 27 1.9 0.7 0.5 0.8 0.2 0.2 1.1 0.4 0.4 2.0 5.8 5.5 10 2 2 3 17 19 4 9 0.62 NA NA 0
1 1 10 42 2.2 1.2 0.9 0.2 0.1 0.4 6.7 2.0 1.0 0.7 3.1 0.4 10 6 5 6 12 21 0 10 0.50 NA NA 0
1 1 1 41 1.2 1.0 0.6 5.1 0.4 0.5 5.1 0.6 1.8 5.3 3.2 3.6 9 8 0 2 16 19 0 8 0.50 NA NA 3
1 2 1 27 0.2 0.1 0.0 2.9 0.0 0.7 4.0 0.0 0.0 8.4 7.0 8.4 10 7 5 3 14 22 10 8 1.00 NA NA -7
1 1 1 25 1.6 0.7 0.0 0.6 0.6 0.6 4.0 0.4 0.9 4.0 4.9 6.6 9 8 4 4 13 15 0 9 0.88 NA NA -2
1 2 0 25 0.0 0.0 0.0 0.0 0.0 0.1 0.0 0.0 4.4 2.0 1.7 1.8 10 8 0 0 15 19 1 10 0.00 NA NA 0
1 1 4 46 0.5 2.1 0.5 0.5 0.3 0.1 7.6 3.9 6.9 1.4 3.9 0.6 10 9 4 4 16 16 7 8 0.38 NA NA 2
1 2 0 21 0.3 0.1 0.1 0.0 0.0 0.0 4.8 0.4 3.9 0.0 2.5 0.0 10 7 3 2 13 22 5 9 0.38 NA NA 0
1 1 11 58 0.7 1.0 0.7 0.0 0.0 0.6 2.5 1.1 1.2 1.8 3.1 7.0 9 7 5 11 20 23 3 8 1.75 NA NA 5
1 2 0 25 0.5 0.9 0.6 0.0 0.0 1.6 1.9 3.0 0.7 7.7 6.5 8.1 10 7 5 16 13 18 3 9 0.75 NA NA -1
1 2 8 41 2.6 0.6 0.9 0.0 0.0 0.0 6.9 1.2 6.6 1.1 5.0 0.3 9 8 5 12 15 21 2 8 1.13 NA NA -3
1 2 1 30 0.3 1.2 2.0 0.0 0.0 1.0 2.5 0.4 0.8 0.4 6.8 1.0 10 3 1 2 15 20 7 9 0.38 NA NA -4
1 1 0 34 0.0 0.8 0.0 1.1 0.7 1.0 0.0 0.0 0.0 0.6 0.5 0.5 10 5 5 7 18 20 4 9 1.50 NA NA -3
1 2 4 27 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.3 2.9 10 4 4 7 17 22 5 7 1.25 NA NA -3
1 2 15 48 1.1 0.0 1.1 1.2 0.4 0.8 2.2 1.9 3.5 3.0 4.0 1.5 10 6 3 6 13 18 2 8 2.25 NA NA -5
1 1 0 29 1.2 0.0 0.0 0.0 0.0 1.5 1.0 0.4 0.7 0.0 2.6 1.0 10 6 1 2 15 20 0 9 0.25 NA NA -3
1 2 0 22 0.0 0.0 0.0 0.4 0.4 0.3 1.0 0.0 0.0 3.8 5.7 6.8 9 7 10 1 13 23 3 7 0.50 NA NA -3
2 2 8 46 0.0 0.0 0.0 0.0 0.0 0.4 7.4 0.0 3.4 0.5 2.2 0.3 10 6 3 1 16 21 0 9 1.50 16413 6.0 -2
2 1 2 29 0.5 0.0 0.0 2.3 0.0 0.9 1.0 0.0 0.0 0.5 1.7 1.3 8 6 2 2 16 19 0 8 0.75 3231 5.4 -1
2 1 0 36 0.4 0.9 0.5 2.0 0.7 3.0 4.7 0.6 1.3 3.1 5.0 4.8 9 6 9 3 19 15 0 8 1.25 12505 4.7 -5
2 2 6 42 1.8 1.3 0.4 1.2 0.3 2.7 5.7 0.5 2.0 3.9 4.2 4.1 8 6 2 0 13 18 0 9 0.13 20567 3.1 -6
2 2 0 25 0.3 2.2 0.3 1.0 0.5 5.6 4.7 2.2 3.2 3.3 4.9 4.3 10 7 2 2 18 20 3 10 0.75 4816 4.8 -1
2 2 2 38 0.0 0.0 0.0 0.0 0.0 0.9 0.0 0.0 0.0 0.0 5.0 1.4 10 6 2 3 16 16 2 10 0.25 24233 1.8 8
2 2 5 31 0.2 0.2 0.0 0.2 0.0 1.4 5.7 0.5 1.3 5.2 1.6 6.0 9 8 3 2 16 20 4 8 0.63 22672 1.8 -6
2 1 4 39 1.5 0.0 1.1 0.0 0.0 0.0 7.3 5.1 5.2 0.0 0.0 0.0 10 8 5 1 13 17 6 9 0.88 44650 1.8 -2
2 1 1 34 0.5 0.2 0.0 0.3 0.2 3.8 1.9 0.7 0.2 2.9 6.1 6.4 10 8 2 7 18 22 1 9 0.38 90077 3.6 -4
2 2 4 26 1.2 0.7 0.7 0.2 0.3 0.5 5.5 1.2 1.0 2.3 5.0 6.2 8 5 1 0 17 19 3 8 0.38 21648 2.7 0
2 2 0 30 0.7 0.5 0.3 0.2 0.1 0.1 1.9 0.6 0.3 0.2 0.2 0.2 9 4 1 3 13 19 1 9 0.38 26590 2.0 0
2 2 3 36 0.5 1.0 0.4 0.0 0.0 0.0 4.6 3.3 3.0 2.6 2.9 1.6 8 5 8 2 18 17 0 5 0.50 29027 3.0 -4
2 1 2 27 0.5 0.4 0.5 0.1 0.2 1.6 1.6 0.7 1.2 4.1 7.6 4.5 10 10 2 2 12 18 0 6 0.50 53526 0.6 5
2 2 1 42 0.9 0.2 0.0 0.4 0.3 0.7 2.6 0.6 0.7 3.3 8.5 4.7 9 3 4 1 16 16 0 9 0.38 107782 1.2 0
2 1 0 37 0.0 0.0 0.0 0.6 0.0 3.2 2.0 2.1 0.0 0.0 9.5 9.0 10 6 1 0 16 18 0 9 0.50 34285 1.6 -3
2 2 5 51 1.3 6.8 2.3 0.0 0.0 0.0 6.4 2.1 3.7 0.0 1.8 0.0 10 8 3 1 14 20 0 3 1.00 1425 2.2 0
2 1 0 24 0.0 0.0 0.0 0.7 0.5 0.4 2.8 0.0 1.4 0.9 3.0 2.1 10 8 2 0 13 18 0 10 0.00 32853 1.2 -7
2 1 5 31 0.1 0.7 0.5 1.6 1.4 1.1 3.0 0.0 0.3 2.4 2.3 3.2 9 6 4 4 18 17 0 8 0.88 26885 5.7 -4
3 1 5 27 1.6 0.6 0.0 2.5 0.1 1.3 4.6 7.7 1.5 1.9 4.3 2.0 10 9 4 2 15 25 5 9 0.50 27116 2.4 -6
3 1 1 28 1.0 0.6 0.4 0.0 0.0 0.0 2.3 0.8 1.1 1.2 2.3 1.8 10 7 0 2 10 15 0 10 0.25 14360 2.1 2
3 2 0 21 0.0 0.1 0.0 0.3 0.7 1.1 1.5 0.0 1.0 1.1 2.5 1.2 10 8 6 2 15 17 0 10 0.87 37782 1.6 0
3 2 6 27 0.0 3.1 0.0 1.3 0.4 4.5 3.9 6.2 2.6 1.3 0.9 2.7 10 4 3 3 13 24 0 10 0.50 1035 5.5 0
3 2 18 53 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.9 5.8 2.3 10 3 4 2 14 19 8 9 0.88 39099 0.0 -4
3 1 5 54 0.0 0.0 0.0 0.9 0.0 4.1 2.0 7.9 6.8 3.2 3.1 3.8 8 7 3 8 15 15 4 7 2.25 90276 2.3 -2
3 2 1 31 2.7 0.5 0.0 1.7 0.0 0.3 9.1 0.6 1.4 6.5 8.3 8.8 9 8 4 3 12 18 6 9 0.75 22095 5.5 3
3 2 2 36 0.5 0.5 0.5 0.0 0.1 0.1 2.0 1.1 1.7 2.3 3.8 2.9 9 7 5 12 14 21 5 7 0.87 53748 3.7 0
3 1 11 33 0.0 0.0 0.0 0.3 0.5 1.1 3.0 1.6 2.0 1.0 2.1 2.3 9 5 4 5 16 20 5 7 0.75 8865 2.0 -6
3 2 2 37 3.8 0.3 2.0 0.7 0.5 1.9 5.1 3.8 3.8 3.8 7.0 5.8 9 8 6 5 13 17 5 7 1.25 10158 5.4 0
3 2 0 41 0.3 0.3 0.1 1.5 0.3 0.3 0.3 0.2 0.3 0.3 0.7 0.2 10 0 2 1 17 16 0 8 0.25 25842 5.1 0
3 2 0 35 1.5 1.7 0.3 1.1 0.7 1.8 4.2 1.3 3.3 5.7 3.9 6.1 10 7 2 5 14 13 4 8 0.63 18272 6.1 -2
3 2 2 24 0.4 0.4 0.0 0.0 0.0 0.0 2.2 0.4 2.1 0.0 7.5 3.3 9 3 1 1 16 22 1 9 0.25 31359 2.2 -1
3 2 1 30 0.6 0.3 0.4 0.5 0.6 0.9 0.3 0.2 0.5 3.3 4.8 5.6 10 4 2 1 13 20 6 8 0.13 45822 0.2 5
3 2 0 35 0.7 2.0 0.0 0.7 0.4 0.5 0.3 0.2 0.0 1.0 4.9 1.0 9 9 3 4 16 19 2 9 0.88 3686 8.3 -7
3 1 5 34 0.0 0.0 0.0 0.2 0.0 1.5 8.1 0.7 0.4 1.5 3.9 5.1 10 4 3 2 15 21 2 8 0.25 65910 1.8 -2
3 2 4 33 0.0 0.0 0.0 0.5 0.2 6.0 6.6 6.4 7.7 3.0 6.7 6.9 10 9 2 7 12 19 1 9 1.00 13096 4.8 -4
3 2 2 32 0.3 0.3 0.3 0.5 0.0 0.0 4.1 2.1 2.4 1.2 2.4 1.7 10 8 3 5 17 18 2 8 1.00 16768 2.8 -5
4 1 0 35 0.2 0.3 0.2 1.3 0.0 1.0 0.2 0.2 0.3 0.5 1.5 2.0 8 6 5 4 16 12 6 8 0.63 NA NA 0
4 1 0 47 0.2 0.2 0.1 1.1 0.0 1.2 2.8 0.2 0.3 2.5 2.1 0.8 10 8 4 4 14 16 3 9 1.63 NA NA -3
4 2 1 29 0.1 0.1 0.1 1.1 0.4 2.7 1.8 0.3 1.4 0.2 4.2 2.3 10 9 3 2 14 16 5 10 0.75 NA NA -2
4 2 7 28 2.4 4.9 0.2 0.6 0.5 0.3 5.3 3.3 0.4 2.2 1.4 0.1 10 4 1 3 12 16 0 9 0.87 NA NA 3
4 1 5 32 0.0 0.0 0.0 0.0 0.0 2.5 3.4 1.9 1.4 3.4 9.2 6.6 10 8 1 2 16 21 4 9 0.62 NA NA -5
4 1 0 35 0.4 0.5 0.3 0.0 0.0 0.0 6.5 1.6 1.0 0.0 3.2 0.5 10 7 6 15 13 21 0 9 1.25 NA NA -8
4 2 0 29 0.9 1.2 1.0 2.9 2.5 3.0 2.3 0.5 0.5 4.9 5.0 5.5 9 5 2 6 17 25 4 8 0.62 NA NA 7
4 1 0 26 0.5 0.0 0.0 0.0 0.0 0.7 0.4 0.0 0.0 0.0 1.3 1.0 9 1 2 3 10 15 6 10 0.75 NA NA 0
4 1 0 32 0.3 1.1 0.4 0.1 0.0 0.0 6.8 5.5 5.9 0.9 0.5 1.0 10 9 6 7 14 15 5 8 1.50 NA NA 4
4 1 0 24 0.0 0.0 0.0 0.0 0.0 0.0 2.5 0.0 0.0 3.0 4.2 3.2 10 4 2 5 12 17 6 9 0.63 NA NA -3
4 1 9 38 2.8 0.0 1.8 0.0 0.0 0.0 1.6 0.0 1.6 3.0 4.3 1.6 9 7 1 1 17 20 2 7 0.38 NA NA 3
4 2 0 32 0.0 1.6 0.9 0.0 0.0 0.0 3.3 2.5 2.7 0.7 7.1 2.6 9 3 3 6 14 22 6 8 0.63 NA NA 0
4 1 4 40 2.0 0.5 3.1 0.4 0.3 0.3 1.5 0.5 3.1 6.7 6.9 6.3 9 8 4 9 14 21 6 8 0.75 NA NA 5
4 2 2 34 0.5 0.0 1.0 2.1 1.5 3.4 4.3 0.0 8.9 3.4 6.8 2.8 10 9 2 1 15 20 4 7 0.50 NA NA 0
4 2 2 28 0.8 0.9 1.0 0.0 0.0 0.0 3.6 1.5 3.0 0.0 4.9 4.8 10 5 2 4 14 21 6 8 1.50 NA NA -5
4 2 0 23 1.6 0.3 0.5 0.0 0.0 1.3 3.2 1.8 0.3 7.1 6.3 6.3 9 2 3 4 18 24 7 9 0.50 NA NA 0
4 2 4 42 2.2 5.0 2.3 0.0 0.0 0.0 5.4 3.4 4.2 1.7 4.8 0.9 9 6 12 7 13 17 3 7 0.50 NA NA -1
4 1 4 54 0.9 0.0 0.0 0.7 0.5 3.3 2.6 0.0 0.7 0.4 1.4 4.9 9 8 3 4 17 21 2 9 0.63 NA NA 0

Here’s a histogram of one variable: Day_Zero_Number_of_Intrustions, which should make sense if you read the description above.

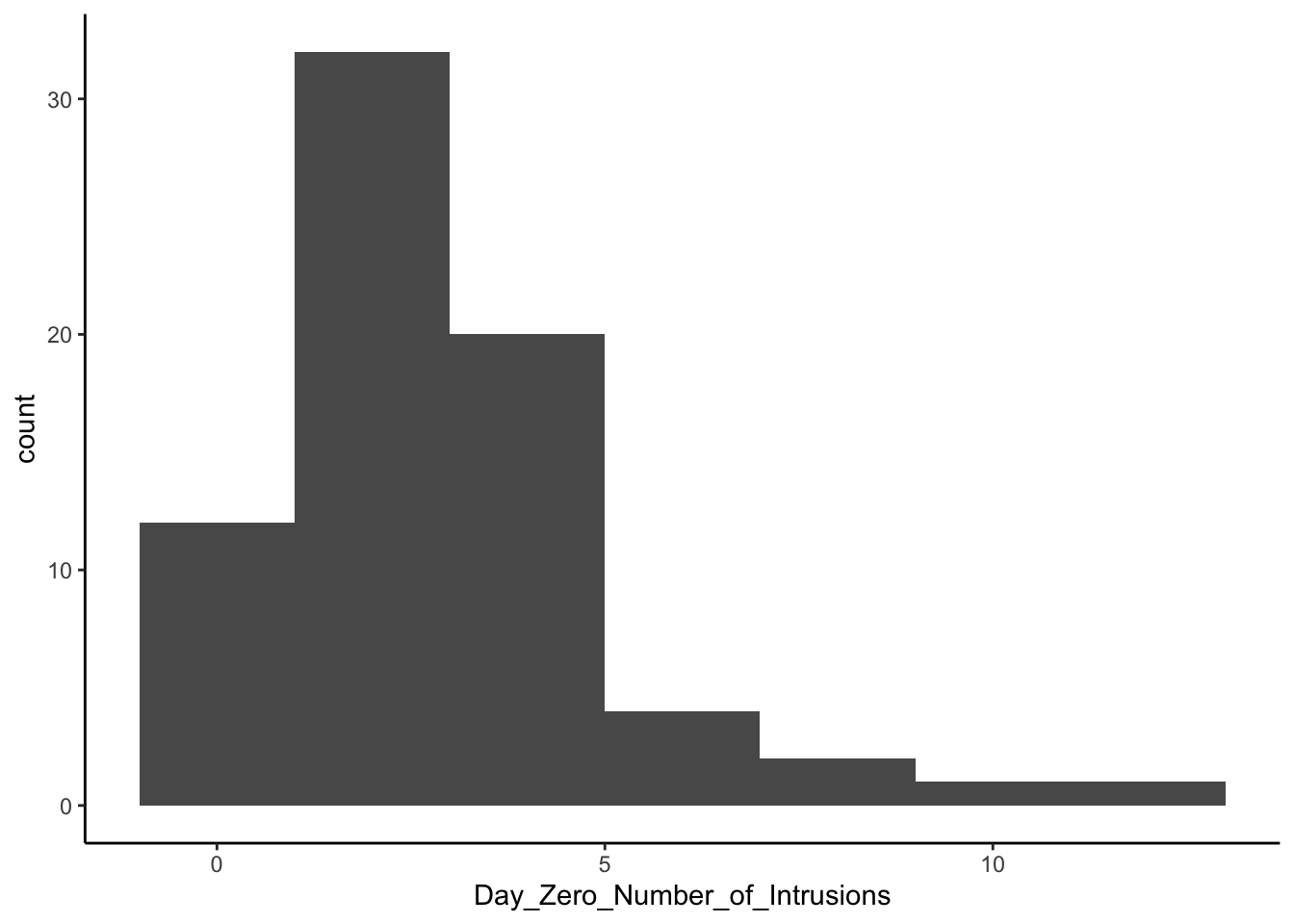
Is the data normal? Close enough, but not terribly normal—probably we don’t need to be concerned in this case, I’d say.

For these data, we SHOULD anticipate finding no difference between groups. Let’s visualize it first. I’ve plotted the data below. Can you recreate this plot in Jamovi? You should be able to create a similar plot. You may want to scroll back up to the section on conditions to see which number corresponds to which condition. Then, under Data, change each number currently listed as Condition to correctly reflect what condition they are in. After, use Descriptives to plot the boxplots with data on top.

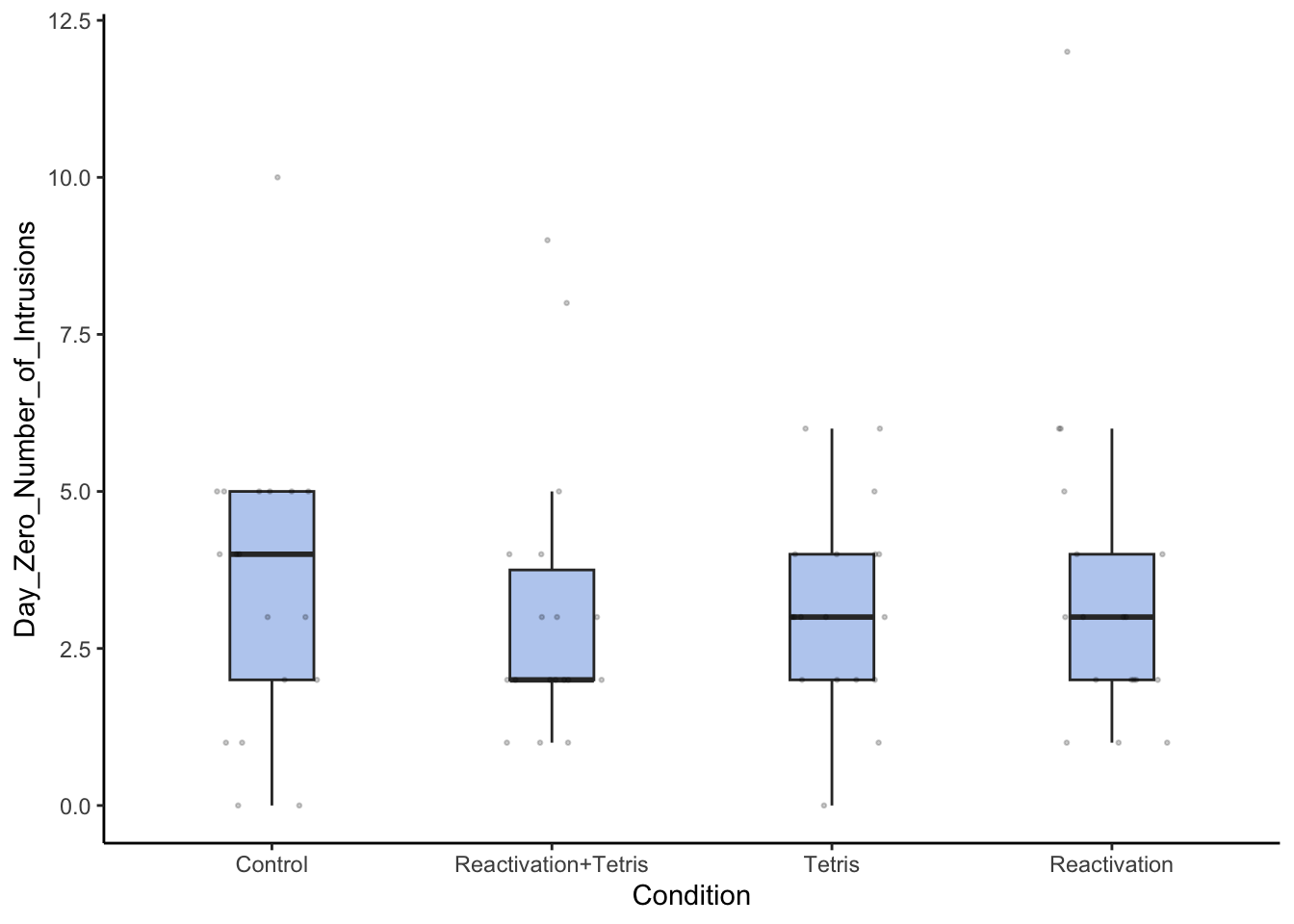
Your plot should have different distribution of the points, which are jittered, but should be quite similar. Export or screenshot the plot you create, and include it in your answer sheet as #1.

Based on this plot, should you expect to see a significant difference? Answer this for #2.

The ANOVA in Jamovi

Run an ANOVA by going to Analyses: ANOVA: One-Way ANOVA. Test what you were looking at in the plot: does condition predict the number of intrusions on Day 0? Turn on the checkbox for Assume Equal (Fisher’s test) and the Descriptives plot. I’ll write up the results for you. Follow this method on other ANOVAs:

There was no significant effect of condition on intrusions on Day 0, \(F(3, 68)=0.16, p=.92\).

As you’ll note, and as we discussed in class, there are two degrees of freedom: first the between-groups df and then the within-groups df. If our test had been significant, we would have written \(p<.05\) instead of giving the p-value.

Like with a t-test, we also report the degrees of freedom. With t-tests, you report something like t(df)=t-value, p < .05 (or \(p=value\)). With an ANOVA, you do the same thing: \(F(\mathit{df_b},\mathit{df_w})=\mathrm{Fvalue}, p<.05\) (or \(p=value\)).

In a more narrative form, I might write:

There was no difference between conditions in the number of intrusions at baseline before the intervention occurred, \(F(3,68)=0.16,p=.92\). Group means varied from \(M=3.17\) intrusions for the Tetris condition to \(M=3.56\) for the control condition, but there was no statistically-significant difference.

What Jamovi gave us here is actually a sort of simplistic version of the ANOVA. It shows us all of the things you need to report as above, but much of the time you’re going to want a bit more: the \(MS_{within}\) and \(MS_{between}\).

What’s going on underneath?

To calculate the ANOVA by getting the component parts, we’ll need to get the pieces to find the F ratio. This section might be useful for understanding how to do the calculations we discussed in class.

I’ll give you the formulae, and then explain getting the mean-squares, and finally the F statistic. You should confirm that you are doing this correctly once you get the \(MS_{within}\) and \(MS_{between}\) from Jamovi directly.

  1. Calculate your degrees of freedom for between and within. \(\mathit{df}_{between}=G-1\) and \(\mathit{df}_{within}=N-G\). Remember that \(N\) is number of participants (total) and \(G\) is number of groups. (Also remember that we just discussed this answer above.) Write these as #3.

  1. Calculate the within-groups mean squares (i.e., variance) in two steps. Remember, \(MS_{within}=\frac{S^2_1+S^2_2+S^2_3+S^2_4}{G}\), that is, it’s the average of the variances of each group.

    1. Get the variance of Day_Zero_Number_of_Intrusions for each Condition under Descriptives. (Yes, it will give you variance if you check that checkbox.)
    2. Write those four variances down somewhere. Then, take their average. That is, add them to one another and then divide by 4. This is \(MS_{within}\). Write it as number 4.

  1. Calculate the between-groups variance. We need 2 numbers per group, and then one average for the whole… and then we’ll plug them into a formula. I recommend writing these down.

    1. Get the whole average: use the Descriptives menu to get the average of Day_Zero_Number_of_Intrusions without any split by or grouping variable. Label this GM, or Grand Mean.

    2. Write down the \(n\) per group and the \(M\) per group. (So, add the split by for Condition back in.)

    3. Those are our nine numbers. Calculate the sum of squares for the between-subjects part of the ANOVA using the following formula: \(SS_{between}=\sum{(n\times{}(M-GM)^2)}\). Essentially, you’re getting the sum of squared deviations but rather than using individual participants’s scores you’re using the group means and subtracting from the grand mean or GM, and then weighting this by the number of participants in each group. For the first one, this is \(18\times{}(3.56-3.32)^2=1.04\). Do the other three, and then sum them up. This is \(SS_{between}\).

    4. Finally, calculate \(MS_{between}\), which is found by \(MS_{between}=\frac{SS_{between}}{df_{between}}\). You already know \(SS_{between}\). \(df_{between}=G-1\), where G is the number of groups. Calculate your \(MS_{between}\). This is #5 on your answer sheet.

Finally, we can find the F statistic, which is the ANOVA’s statistic. This part is straightforward; it’s a ratio.

\[F=\frac{S_{between}^2}{S_{within}^2}=\frac{MS_{between}}{MS_{within}}\]

So, calculate F with the answers you found in the previous two questions.

You should get the same F-value we previously found from Jamovi. Because the between-participants variance is smaller than the within-participants variance, F will be small – not big enough to reject our null. (We discussed how to use an F-table in class, but you don’t need to pull it out here.)

Get the ANOVA table in Jamovi

Okay, back to doing this fully in Jamovi. Go to Analyses: ANOVA: ANOVA. ( Note: This is not just “One-Way”.) Condition is your fixed factor. Day_Zero_Number_of_Intrusions is still your DV. You should see a table similar to this one:

term Sum of Squares df Mean Square F p
Condition 2.49 3 0.829 0.163 0.921
Residuals 345.17 68 5.076

Where it says “Condition”, that’s the between-groups row. And where it says “Residuals”—that’s the within-groups bit.

Do the values for \(MS\) and \(F\) match what you calculated? If not, consider revisiting your calculations and figuring out what went wrong.

Do it on your own

  1. Run two ANOVAs: one asking whether Condition determines the number of intrusive thoughts in the days after the intervention (Days_One_to_Seven_Number_of_Intrusions), and the second asking whether Condition impacts the responses on the task that was designed to measure intrusive thoughts (Number_of_Provocation_Task_Intrusions).

    For each ANOVA, you should report the results as we did in the tutorial—complete with means and the \(F(df_1,df_2)=value,p<.05\) or \(p=value\). These are #6a and #6b.

  2. For the provocation task test’s results, scroll down in Jamovi under the ANOVA menu and click the drop-down for Estimated Marginal Means. Move Condition to Term 1, check off “observed scores,” and look at the resulting plot. Export/screenshot/copy it into your answer sheet. Then answer: which group(s) are different from the other(s)? This is #7.

Pairwise tests

I told you in class that you shouldn’t repeatedly use t-tests because of the fact that doing so increases your Type I error rate (i.e., risk of false positives). However, you can do what are called planned comparisons. After a significant result on an ANOVA, you may compare the condition of interest against the others if you intended to do so before starting. (This is one more reason why preregistration is so important!) Usually, even when you’ve planned to do comparisons, you should do a correction for the planned comparison. In this case, we want to compare the Reactivation + Tetris condition to the others. (This was the one we hoped would work.) We don’t need to make every other comparison.

In your ANOVA menu, you can do this easily. Let’s stick to the previous ANOVA looking at the provocation task. Scroll down to where it says “Post-hoc tests” and click the checkbox. Put Condition in the right side of the test window. Make sure “Tukey” is checked ON under Correction (and “Uncorrect” is not checked). Check ON the Cohen’s d for Effect Size as well. In the results, you’ll see a few corrected t-test values for each possible (pairwise) comparison. The final column is the corrected p-value; the penultimate is the t-value. Pick one that’s statistically significant (i.e., where \(p<.05\)) based on the Tukey-corrected p-value.

  1. For #8, write up the results of the significant t-test, just using what Jamovi gave you.

  2. Then, under Data, filter to just those two conditions. Remember that you need to repeat the variable name (Condition) each time you set it == to the condition names. Remember, too, that spelling, capitalization, and spacing all matter.

    Once the filter is working, run an independent-samples t-test predicting Number_of_Provocation_Task_Intrusions by Condition. For #9, write up these results, and then answer: what (if anything) is different in this non-corrected result?

That’s it.

Reuse

Citation

BibTeX citation:
@online{dainer-best2024,
  author = {Dainer-Best, Justin},
  title = {One-Way {ANOVA} {(Lab} 9)},
  date = {2024-04-04},
  url = {https://faculty.bard.edu/jdainerbest/stats/labs//posts/09-one-way-anova},
  langid = {en}
}
For attribution, please cite this work as:
Dainer-Best, Justin. 2024. “One-Way ANOVA (Lab 9).” April 4, 2024. https://faculty.bard.edu/jdainerbest/stats/labs//posts/09-one-way-anova.