| Month | Date | Two.weeks.prior.to.outbreak.only | Nationwide.Republican.Support | Nationwide.Democratic.Support | Voter.Intention.Index | Voter.Intention.Change.Index | Daily.Ebola.Search.Volume | Ebola.Search.Volume.Index | Daily.ISIS.Search.Volume | ISIS.Search.Volume.Index | DJIA | LexisNexisNewsVolume | LexisNexisNewsVolumeWeek | filter_. | time |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 1 | 0 | NA | NA | NA | NA | 3 | 2.86 | 14 | NA | NA | 23 | 37.57 | 1 | 2014-09-01 |
| 9 | 2 | 0 | NA | NA | NA | NA | 5 | 3.14 | 37 | NA | 17067.56 | 38 | 34.86 | 1 | 2014-09-02 |
| 9 | 3 | 0 | NA | NA | NA | NA | 6 | 3.57 | 48 | NA | 17078.28 | 52 | 36.43 | 1 | 2014-09-03 |
| 9 | 4 | 0 | NA | NA | NA | NA | 4 | 3.71 | 37 | NA | 17069.58 | 50 | 37.14 | 1 | 2014-09-04 |
| 9 | 5 | 0 | NA | NA | NA | NA | 4 | 3.86 | 27 | NA | 17137.36 | 51 | 40.00 | 1 | 2014-09-05 |
| 9 | 6 | 0 | NA | NA | NA | NA | 3 | 3.57 | 23 | NA | NA | 31 | 38.86 | 1 | 2014-09-06 |
| 9 | 7 | 0 | 43.7 | 42.3 | 1.4 | NA | 3 | 4.00 | 24 | 30.000000 | NA | 23 | 38.29 | 1 | 2014-09-07 |
| 9 | 8 | 0 | NA | NA | NA | NA | 3 | 4.00 | 23 | 31.285714 | 17111.42 | 30 | 39.29 | 1 | 2014-09-08 |
| 9 | 9 | 0 | 43.7 | 42.5 | 1.2 | NA | 4 | 3.86 | 19 | 28.714286 | 17013.87 | 74 | 44.43 | 1 | 2014-09-09 |
| 9 | 10 | 0 | NA | NA | NA | NA | 3 | 3.43 | 27 | 25.714286 | 17068.71 | 42 | 43.00 | 1 | 2014-09-10 |
| 9 | 11 | 0 | NA | NA | NA | NA | 3 | 3.29 | 100 | 34.714286 | 17049.00 | 32 | 40.43 | 1 | 2014-09-11 |
| 9 | 12 | 0 | NA | NA | NA | NA | 3 | 3.14 | 36 | 36.000000 | 16987.51 | 52 | 40.57 | 1 | 2014-09-12 |
| 9 | 13 | 0 | NA | NA | NA | NA | 3 | 3.14 | 25 | 36.285714 | NA | 29 | 40.29 | 1 | 2014-09-13 |
| 9 | 14 | 0 | 43.9 | 42.9 | 1.0 | -0.4 | 2 | 3.00 | 52 | 40.285714 | NA | 29 | 41.14 | 1 | 2014-09-14 |
| 9 | 15 | 0 | NA | NA | NA | NA | 3 | 3.00 | 28 | 41.000000 | 17031.14 | 40 | 42.57 | 1 | 2014-09-15 |
| 9 | 16 | 0 | NA | NA | NA | NA | 5 | 3.14 | 23 | 41.571429 | 17131.97 | 89 | 44.71 | 1 | 2014-09-16 |
| 9 | 17 | 0 | NA | NA | NA | NA | 6 | 3.57 | 19 | 40.428571 | 17156.85 | 128 | 57.00 | 1 | 2014-09-17 |
| 9 | 18 | 0 | 43.8 | 43.2 | 0.6 | NA | 3 | 3.57 | 22 | 29.285714 | 17265.99 | 140 | 72.43 | 1 | 2014-09-18 |
| 9 | 19 | 0 | NA | NA | NA | NA | 4 | 3.71 | 18 | 26.714286 | 17279.74 | 71 | 75.14 | 1 | 2014-09-19 |
| 9 | 20 | 0 | NA | NA | NA | NA | 2 | 3.57 | 13 | 25.000000 | NA | 57 | 79.14 | 1 | 2014-09-20 |
| 9 | 21 | 0 | 43.7 | 43.3 | 0.4 | -0.6 | 2 | 3.57 | 16 | 19.857143 | NA | 36 | 80.14 | 1 | 2014-09-21 |
| 9 | 22 | 0 | NA | NA | NA | NA | 3 | 3.57 | 16 | 18.142857 | 17172.68 | 85 | 86.57 | 1 | 2014-09-22 |
| 9 | 23 | 0 | NA | NA | NA | NA | 4 | 3.43 | 33 | 19.571429 | 17055.87 | 74 | 84.43 | 1 | 2014-09-23 |
| 9 | 24 | 1 | NA | NA | NA | NA | 4 | 3.14 | 24 | 20.285714 | 17210.06 | 90 | 79.00 | 1 | 2014-09-24 |
| 9 | 25 | 1 | 43.1 | 43.5 | -0.4 | -1.0 | 4 | 3.29 | 22 | 20.285714 | 16945.80 | 92 | 72.14 | 1 | 2014-09-25 |
| 9 | 26 | 1 | NA | NA | NA | NA | 4 | 3.29 | 22 | 20.857143 | 17113.15 | 113 | 78.14 | 1 | 2014-09-26 |
| 9 | 27 | 1 | NA | NA | NA | NA | 3 | 3.43 | 15 | 21.142857 | NA | 69 | 79.86 | 1 | 2014-09-27 |
| 9 | 28 | 1 | 43.3 | 43.6 | -0.3 | -0.7 | 6 | 4.00 | 14 | 20.857143 | NA | 57 | 82.86 | 1 | 2014-09-28 |
| 9 | 29 | 1 | 43.4 | 43.6 | -0.2 | NA | 5 | 4.29 | 13 | 20.428571 | 17071.22 | 55 | 78.57 | 1 | 2014-09-29 |
| 9 | 30 | 1 | 43.5 | 43.6 | -0.1 | NA | 22 | 6.86 | 11 | 17.285714 | 17042.90 | 57 | 76.14 | 1 | 2014-09-30 |
| 10 | 1 | 1 | NA | NA | NA | NA | 50 | 13.43 | 10 | 15.285714 | 16804.71 | 197 | 91.43 | 0 | 2014-10-01 |
| 10 | 2 | 1 | 43.8 | 43.7 | 0.1 | 0.5 | 68 | 22.57 | 8 | 13.285714 | 16801.05 | 298 | 120.86 | 0 | 2014-10-02 |
| 10 | 3 | 1 | NA | NA | NA | NA | 66 | 31.43 | 8 | 11.285714 | 17009.69 | 237 | 138.57 | 0 | 2014-10-03 |
| 10 | 4 | 1 | NA | NA | NA | NA | 52 | 38.43 | 11 | 10.714286 | NA | 160 | 151.57 | 0 | 2014-10-04 |
| 10 | 5 | 1 | 44.3 | 43.6 | 0.7 | 1.0 | 41 | 43.43 | 9 | 10.000000 | NA | 125 | 161.29 | 0 | 2014-10-05 |
| 10 | 6 | 1 | 44.4 | 43.6 | 0.8 | 1.0 | 43 | 48.86 | 9 | 9.428571 | 16991.91 | 118 | 170.29 | 0 | 2014-10-06 |
| 10 | 7 | 1 | 44.5 | 43.5 | 1.0 | 1.1 | 35 | 50.71 | 9 | 9.142857 | 16719.39 | 186 | 188.71 | 0 | 2014-10-07 |
| 10 | 8 | 0 | NA | NA | NA | NA | 52 | 51.00 | 9 | 9.000000 | 16994.22 | 208 | 190.29 | 0 | 2014-10-08 |
| 10 | 9 | 0 | 44.6 | 43.5 | 1.1 | 1.0 | 57 | 49.43 | 9 | 9.142857 | 16695.25 | 314 | 192.57 | 0 | 2014-10-09 |
| 10 | 10 | 0 | NA | NA | NA | NA | 62 | 48.86 | 7 | 9.000000 | 16544.10 | 250 | 194.43 | 0 | 2014-10-10 |
| 10 | 11 | 0 | NA | NA | NA | NA | 37 | 46.71 | 9 | 8.714286 | NA | 175 | 196.57 | 0 | 2014-10-11 |
| 10 | 12 | 0 | 44.7 | 43.4 | 1.3 | 0.6 | 51 | 48.14 | 10 | 8.857143 | NA | 157 | 201.14 | 0 | 2014-10-12 |
| 10 | 13 | 0 | NA | NA | NA | NA | 57 | 50.14 | 8 | 8.714286 | 16321.07 | 315 | 229.29 | 0 | 2014-10-13 |
| 10 | 14 | 0 | 44.9 | 43.5 | 1.4 | 0.4 | 57 | 53.29 | 7 | 8.428571 | 16315.19 | 322 | 248.71 | 0 | 2014-10-14 |
| 10 | 15 | 0 | NA | NA | NA | NA | 92 | 59.00 | 8 | 8.285714 | 16141.74 | 353 | 269.43 | 0 | 2014-10-15 |
| 10 | 16 | 0 | 45.1 | 43.5 | 1.6 | 0.5 | 100 | 65.14 | 6 | 7.857143 | 16117.24 | 512 | 297.71 | 0 | 2014-10-16 |
| 10 | 17 | 0 | NA | NA | NA | NA | 83 | 68.14 | 7 | 7.857143 | 16380.41 | 583 | 345.29 | 0 | 2014-10-17 |
| 10 | 18 | 0 | NA | NA | NA | NA | 56 | 70.86 | 6 | 7.428571 | NA | 402 | 377.71 | 0 | 2014-10-18 |
| 10 | 19 | 0 | NA | NA | NA | NA | 38 | 69.00 | 5 | 6.714286 | NA | 269 | 393.71 | 0 | 2014-10-19 |
| 10 | 20 | 0 | 45.4 | 43.5 | 1.9 | NA | 35 | 65.86 | 5 | 6.285714 | 16399.67 | 384 | 403.57 | 0 | 2014-10-20 |
| 10 | 21 | 0 | 45.5 | 43.5 | 2.0 | 0.6 | 40 | 63.43 | 5 | 6.000000 | 16614.81 | 359 | 408.86 | 0 | 2014-10-21 |
| 10 | 22 | 0 | NA | NA | NA | NA | 28 | 54.29 | 4 | 5.428571 | 16461.32 | 327 | 405.14 | 0 | 2014-10-22 |
| 10 | 23 | 0 | 45.6 | 43.5 | 2.1 | 0.5 | 22 | 43.14 | 6 | 5.428571 | 16677.90 | 273 | 371.00 | 0 | 2014-10-23 |
| 10 | 24 | 0 | NA | NA | NA | NA | 48 | 38.14 | 5 | 5.142857 | 16805.41 | 388 | 343.14 | 0 | 2014-10-24 |
| 10 | 25 | 0 | NA | NA | NA | NA | 25 | 33.71 | 4 | 4.857143 | NA | 302 | 328.86 | 0 | 2014-10-25 |
| 10 | 26 | 0 | 45.7 | 43.5 | 2.2 | NA | 20 | 31.14 | 4 | 4.714286 | NA | 197 | 318.57 | 0 | 2014-10-26 |
| 10 | 27 | 0 | 45.8 | 43.5 | 2.3 | 0.4 | 23 | 29.43 | 4 | 4.571429 | 16817.94 | 294 | 305.71 | 0 | 2014-10-27 |
| 10 | 28 | 0 | NA | NA | NA | NA | 24 | 27.14 | 3 | 4.285714 | 17005.75 | 327 | 301.14 | 0 | 2014-10-28 |
| 10 | 29 | 0 | NA | NA | NA | NA | 22 | 26.29 | 4 | 4.285714 | 16974.31 | 259 | 291.43 | 0 | 2014-10-29 |
| 10 | 30 | 0 | 45.9 | 43.6 | 2.3 | 0.2 | 18 | 25.71 | 4 | 4.000000 | 17195.42 | 293 | 294.29 | 0 | 2014-10-30 |
| 10 | 31 | 0 | NA | NA | NA | NA | 16 | 21.14 | 4 | 3.857143 | 17390.52 | 281 | 279.00 | 0 | 2014-10-31 |
| 11 | 1 | 0 | 46.0 | 43.6 | 2.4 | NA | 11 | 19.14 | 3 | 3.714286 | NA | 218 | 267.00 | 0 | 2014-11-01 |
| 11 | 2 | 0 | NA | NA | NA | NA | 11 | 17.86 | 4 | 3.714286 | NA | 150 | 260.29 | 0 | 2014-11-02 |
| 11 | 3 | 0 | NA | NA | NA | NA | 36 | 19.71 | 4 | 3.714286 | 17366.24 | 214 | 248.86 | 0 | 2014-11-03 |
| 11 | 4 | 0 | NA | NA | NA | NA | 15 | 18.43 | 4 | 3.857143 | 17383.84 | 118 | 219.00 | 0 | 2014-11-04 |
Objectives
Today’s lab’s objectives are to:
- Learn about regressions and correlations
- Do some basic plotting relating to them
- Learn how to conduct a regression and a correlation in Jamovi
You’ll turn in an “answer sheet” on Brightspace. Please turn that in by the end of the weekend.
Correlations and regressions
A correlation examines the relationship between two numeric variables, while a regression lets us predict a score on an outcome (criterion) variable from one or multiple predictors. The latter is also the statistical procedure for finding the best-fitting linear line to aid in that prediction.
Regressions and correlations by definition use two, paired numeric variables. There must be some specific relationship between them.
In today’s lab, we’ll be using data from Beall, Hofer, & Shaller (2016). The article is:
Beall, A. T., Hofer, M. K., & Shaller, M. (2016). Infections and elections: Did an Ebola outbreak influence the 2014 U.S. federal elections (and if so, how)? Psychological Science, 27, 595-605. https://doi.org/10.1177/0956797616628861
(Thanks to Kevin P. McIntyre’s curation of this data.)
The experiment
Beall, Hofer, and Schaller (2016) wanted to determine whether the outbreak of Ebola in 2014 increased support for more conservative electoral candidates. They didn’t look at people in particular—they looked at the frequency of web searches for the term “Ebola” before and after the outbreak, and they looked at polls on support for Republicans and Democrats in their U.S. House of Representatives races during the same time.
Their data is thus paired by date—it’s not paired by the individual like much of the work we’re interested in is.
The researchers asked: is the psychological salience of Ebola associated with an increased intention to vote for Republican candidates?
Read the question below, and decide what you think before clicking for the answer.
What is the framing of this question for a research hypothesis and a null hypothesis??
Research hypothesis: There is some relationship (\(r\neq0\)) between Ebola searches and conservative voting intentions
Null hypothesis: There is no relationship (\(r=0\)) between Ebola searches and conservative voting intentions
By definition, we almost always just say “not equal” rather than \(r>0\) or \(r<0\), which means we’re defaulting to a 2-tailed hypothesis.
Explore the data
Scroll through the data briefly (up and down or right-to-left).
You can use the above interface to look through the data. There are several variables and several NAs. You’ll get to look at some of the other variables later, but for the moment, we’re going to look at the Voter.Intention.Index and the Ebola.Search.Volume.Index—you can read the paper for more info, but these two have been created as indexes of the main ideas.
- The
Voter.Intention.Indexis created as the difference between the percentage of voters who planned to vote for a Democrat and those who intended to vote for a Republican; thus a positive value indicates preference for Republican candidates. - The
Ebola.Search.Volume.Indexinvolves online searches for the term “Ebola”.
Let’s start by looking at the way they changed over time. Take a look at the image below.
What do you see in the plot? Discuss with a classmate, then click through.
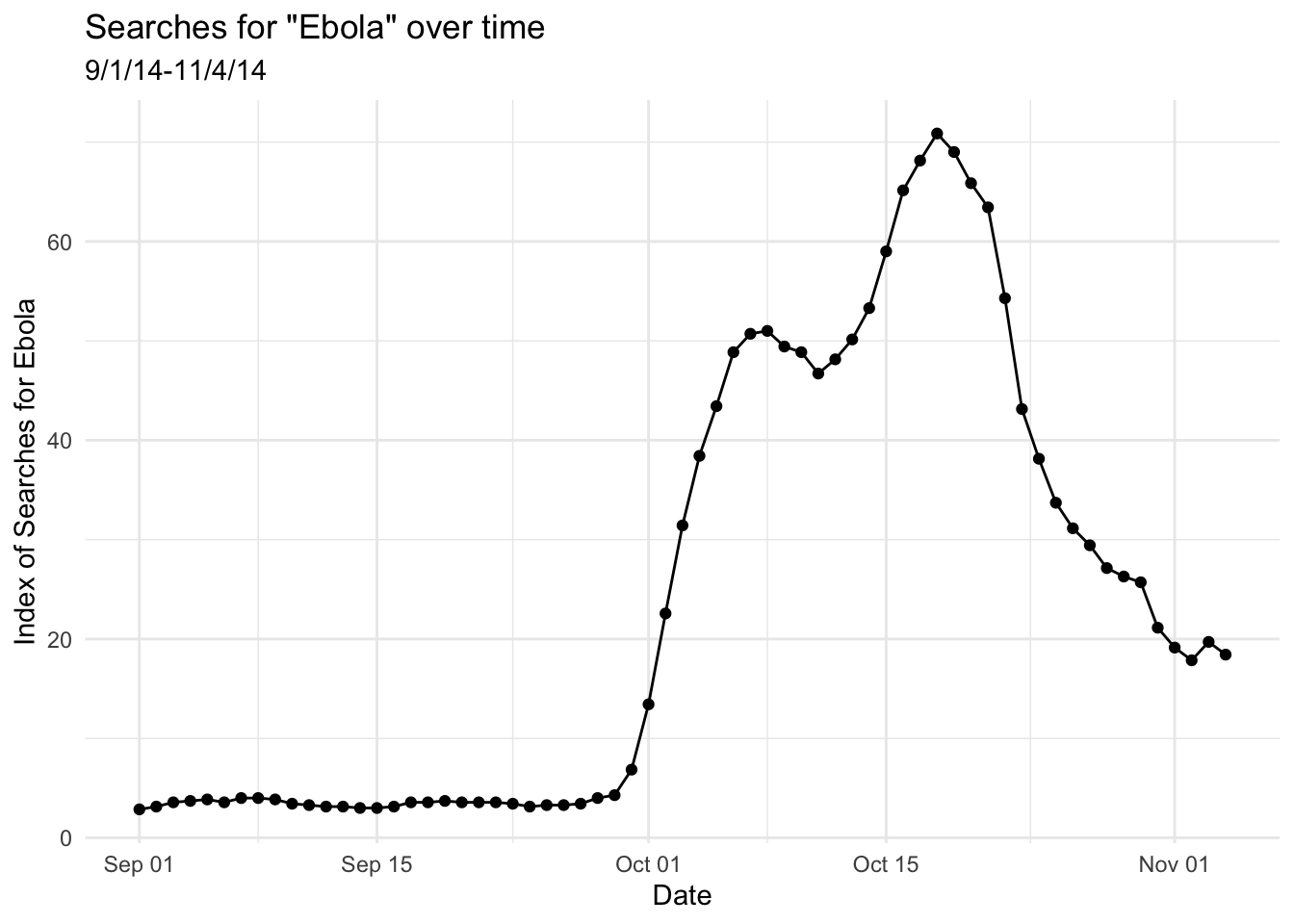
My conclusion: there were rare searches for the term “Ebola” for much of early September, 2014, and then a significant increase in early October of 2014, followed by a decline after the peak in mid-October. Why do you think this might have been? There’s a wikipedia article about the 2014 events; you can read it if you’re curious.
On another side of things, an index of a variety of polls conducted on several days shows voters intentions over that same period. (You’ll note that there are fewer points.) What do you see?
What do you see in the plot? Discuss with a classmate, then click through.
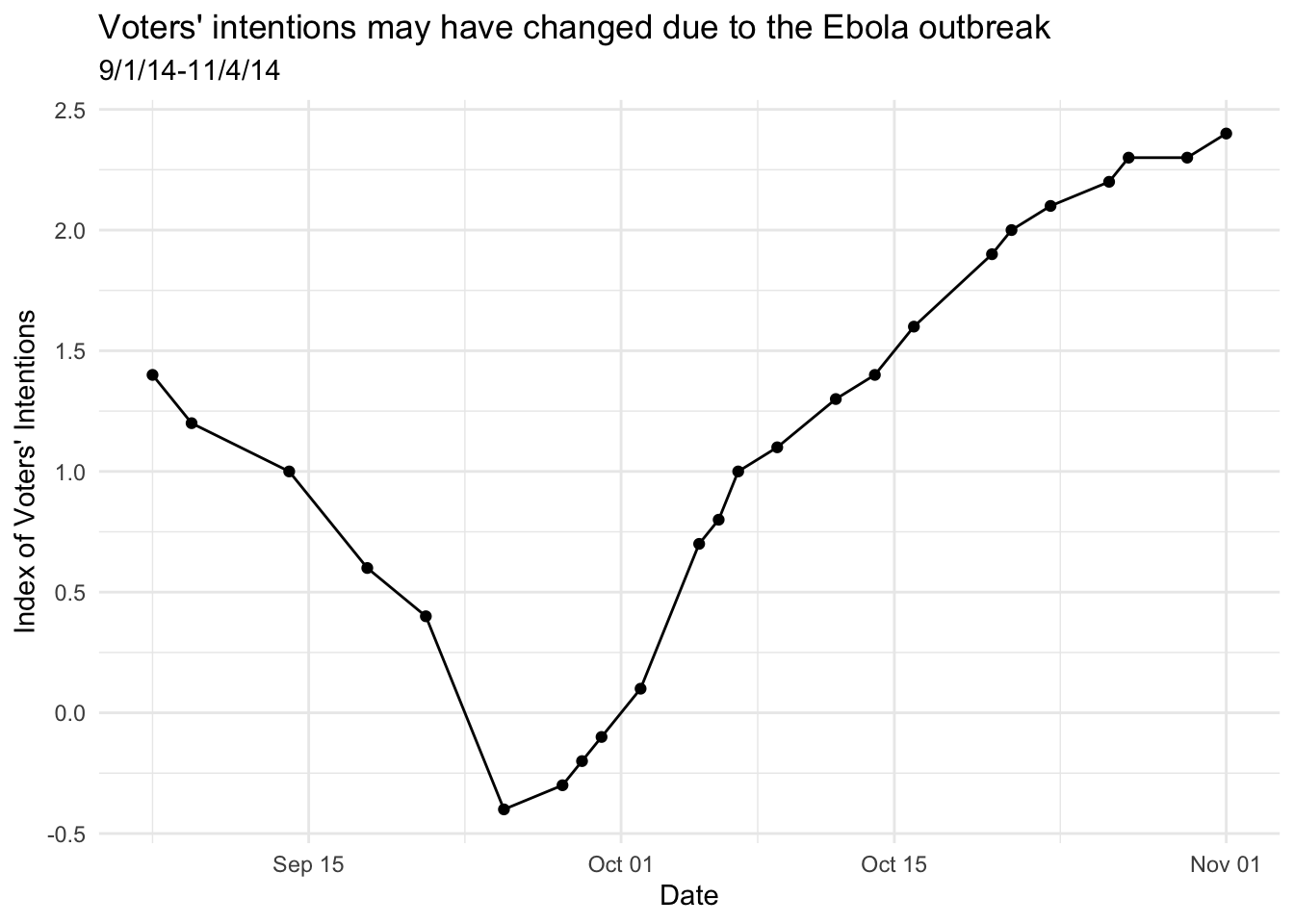
My conclusion: Voter intentions changed in sort of the same timeline, but in the opposite direction. (And maybe at a slightly different timeline?) Higher scores here mean a larger chance of voting for Republican (than Democrat) candidates. So from shortly before October 1, polls showed an increase in likelihood of voting for Republicans.
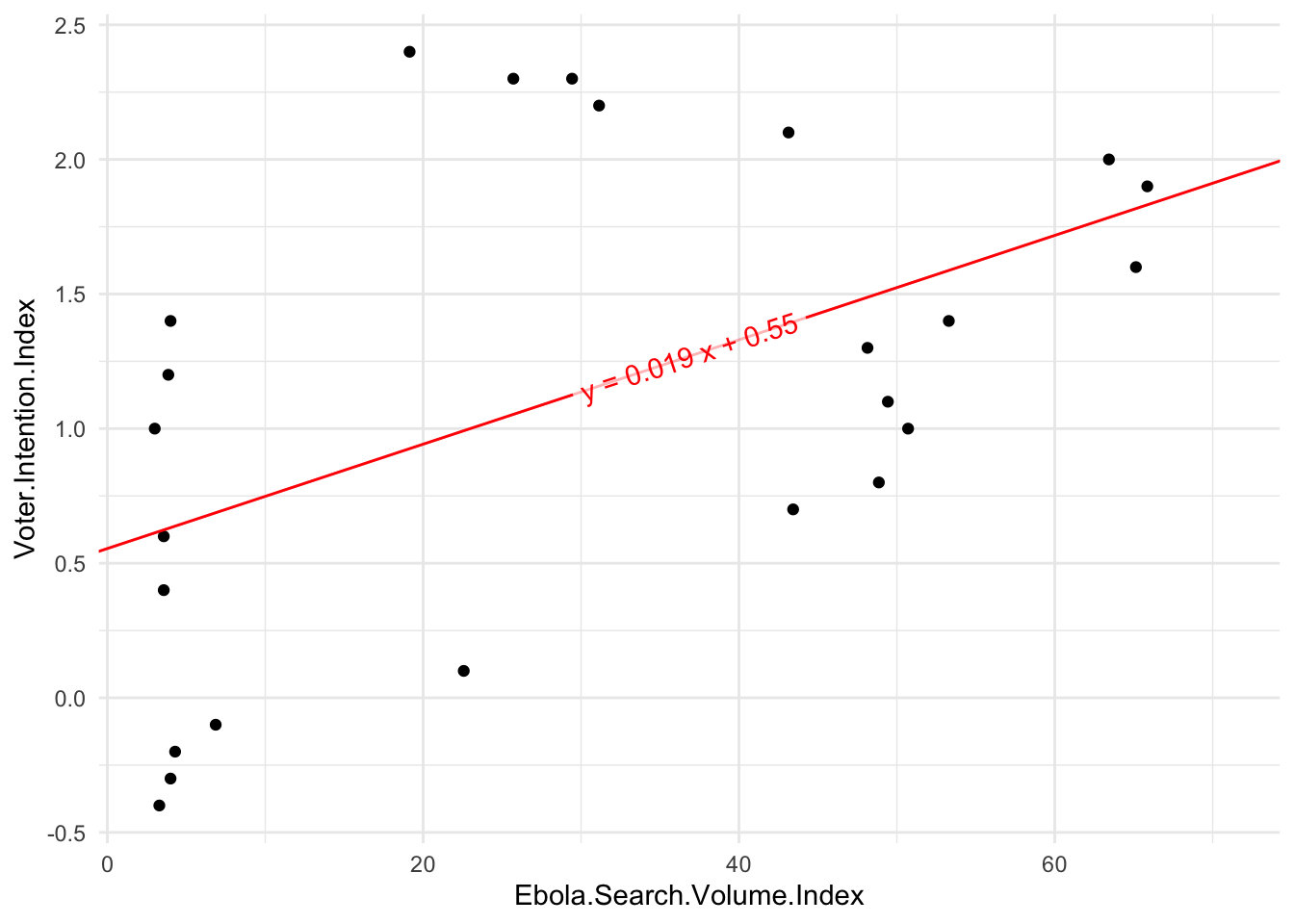
You may say: okay, but the correlation we’re interested in is not between these variables and the date, but rather with each other—and you’re quite right. One way to look at these together is to plot them against one another. This would be a scatterplot!
Do you think there’s a pattern here? Where would the line of best fit go? Is there a correlation? Click through to see the line.
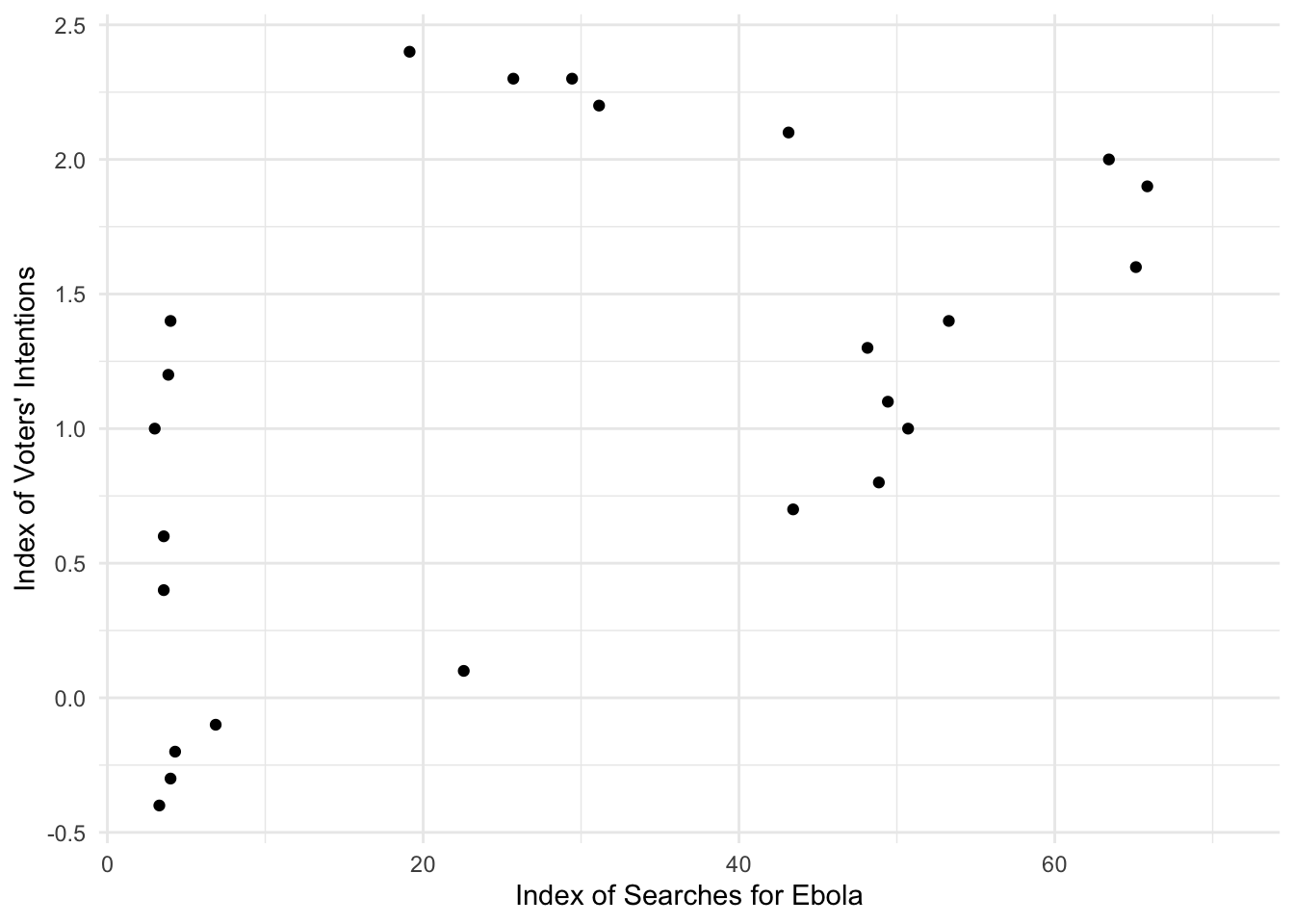
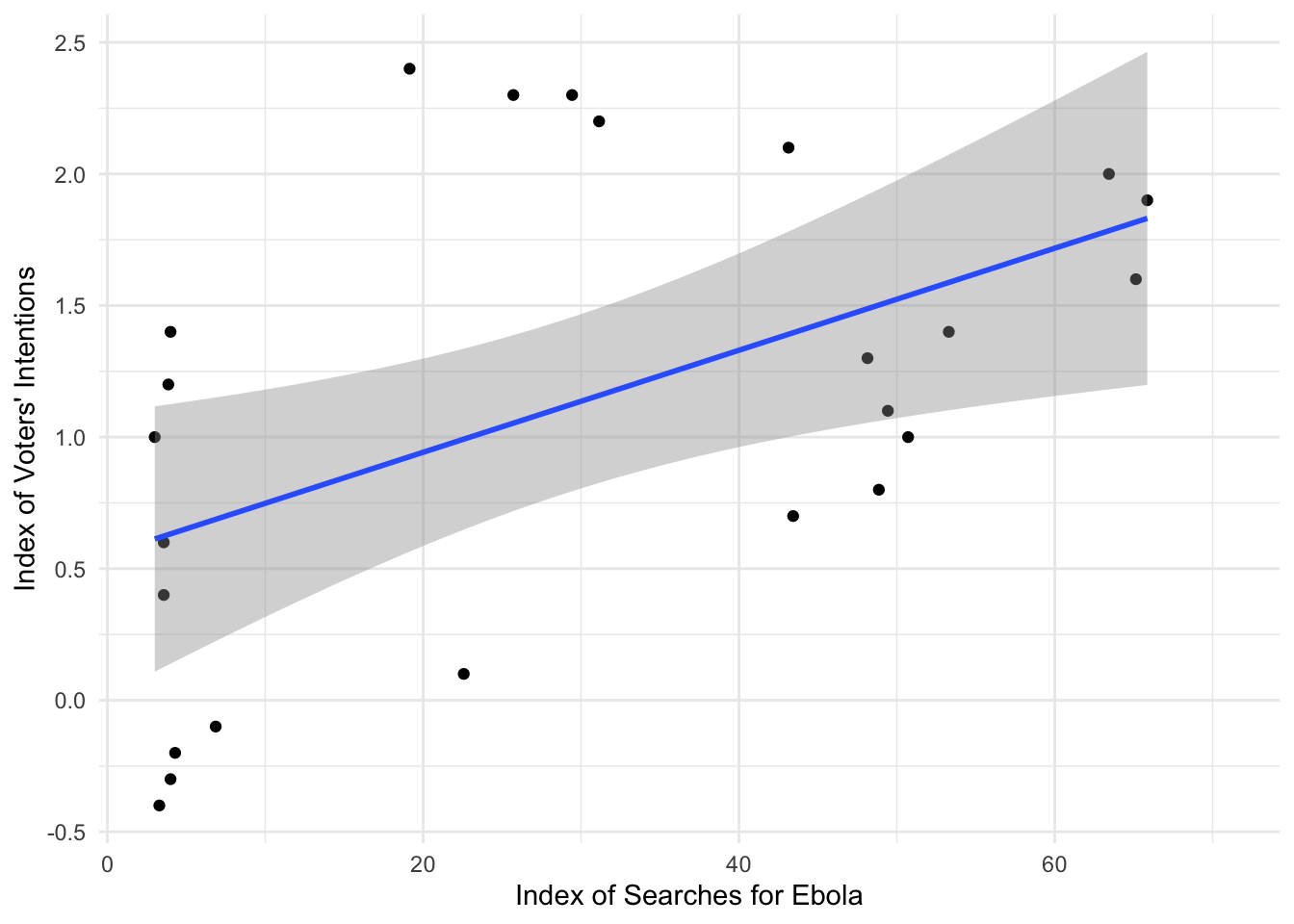
Yes, it looks like there may be a linear correlation. The gray area represents the confidence interval—yep, like the 95% confidence intervals we’ve discussed. The blue line is the line of best fit—the regression line.
You’ll also see that a correlation doesn’t actually care about date. It’s just pairing the two variables based on something they have in common. There are analyses which would take the date into account (or at least think about time as linear), but that’s more complex than what we’re doing today.
I hope that you can see that there’s probably some connection between these points, but one more thing we could do is plot them against each other over time. As I said in the “info” note above, this isn’t necessarily what a correlation is testing, but let’s take a look.
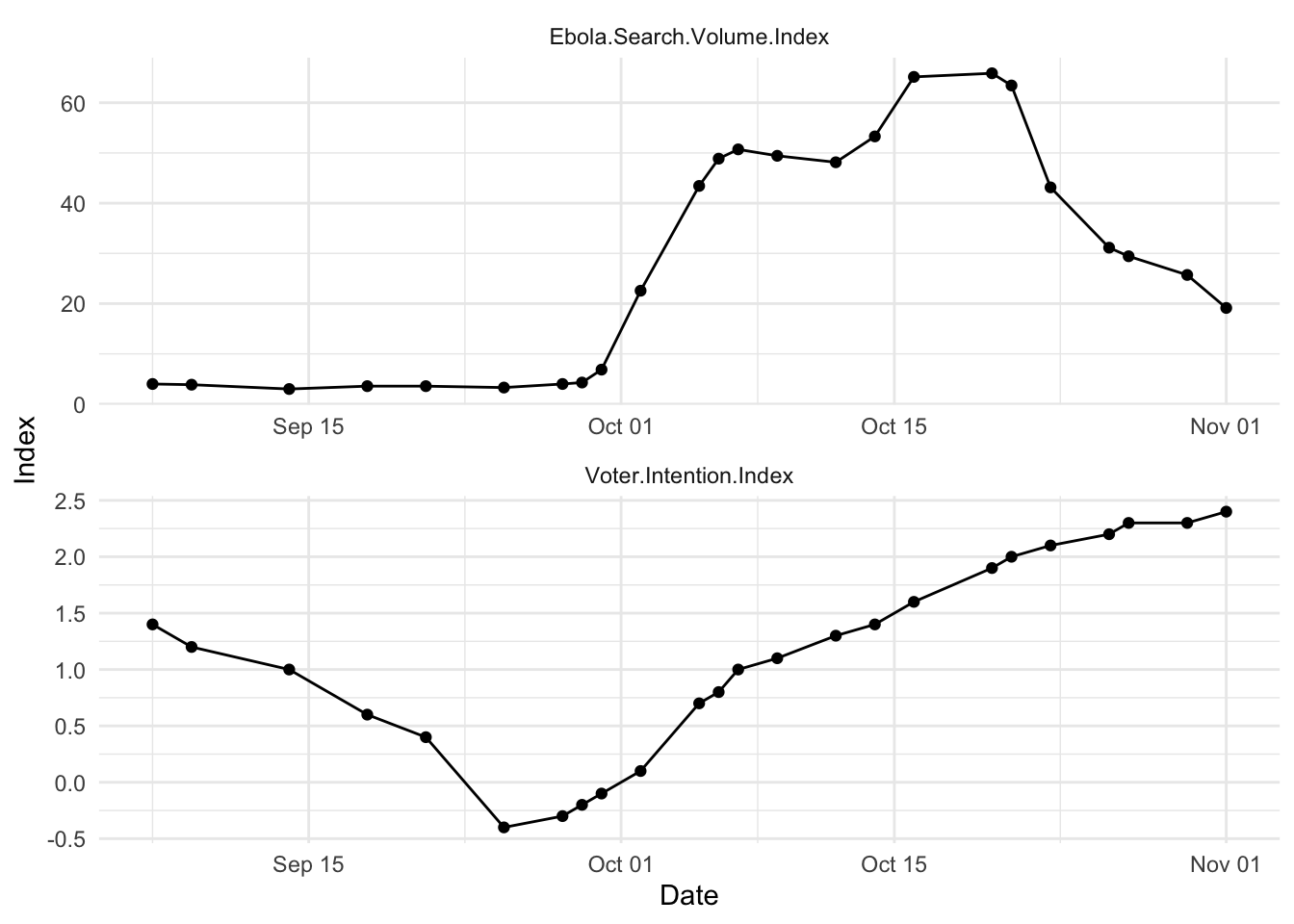
Again, discuss with a classmate. Do you think there’s a correlation over time? From this, do you think there’s a date-based pattern? Do these rise and fall together?
Onward to the tests.
Running correlations
As we discussed in class, we can do both a correlation and a regression in Jamovi here.
Are Ebola.Search.Volume.Index and Voter.Intention.Index correlated in a statistically-significant way? In Jamovi, you’ll go to Analyses, click on Regression, and then click on “Correlation Matrix.” Put both/all variables in the right side and they’ll form a matrix (here, just a table) of values. (Don’t do this yet; I’ve yet to give you any data.)
Jamovi’s results give a table that looks something like this:
| Pearson's r | df | p.value |
|---|---|---|
| 0.505 | 22.000 | 0.012 |
Is the result of the correlation statistically significant?
Yes, it is statistically significant because \(p<.05\)
The test shows a p-value of 0.012; this is less than .05 and therefore you should reject the null hypothesis. The correlation is statistically-significant.
In class, we talked about the technical formula for a Pearson’s correlation. Although as I said in class, you won’t need to calculate this, this is a formula you could use to calculate the correlation coefficient by hand.
\[r=\frac{\sum{z_X\times{}z_Y}}{N-1}\]
This is “the average of the sum of the product of the z-scores”. And yes, it’s \(N-1\) on the bottom.
We can do the summed product of z-scores with these data. The mean of Ebola.Search.Volume.Index is 28.99 and the mean of Voter.Intention.Index is 1.12. We can use the formula of \(z=\frac{X-M}{SD}\) to calculate all the z-scores, and their products (\(z_X\times{}z_Y\)). I’m not going to force you to do it yourself in Google Sheets or Excel; I’ve done it below:
| Ebola.Search.Volume.Index | Voter.Intention.Index | z_search | z_intention | z_product |
|---|---|---|---|---|
| 4.00 | 1.4 | -1.08234694 | 0.31980326 | -0.34613808 |
| 3.86 | 1.2 | -1.08840950 | 0.09405978 | -0.10237556 |
| 3.00 | 1.0 | -1.12565092 | -0.13168370 | 0.14822987 |
| 3.57 | 0.6 | -1.10096766 | -0.58317065 | 0.64205203 |
| 3.57 | 0.4 | -1.10096766 | -0.80891413 | 0.89058830 |
| 3.29 | -0.4 | -1.11309277 | -1.71188805 | 1.90549021 |
| 4.00 | -0.3 | -1.08234694 | -1.59901631 | 1.73069041 |
| 4.29 | -0.2 | -1.06978879 | -1.48614457 | 1.58986080 |
| 6.86 | -0.1 | -0.95849755 | -1.37327283 | 1.31627865 |
| 22.57 | 0.1 | -0.27819200 | -1.14752935 | 0.31923348 |
| 43.43 | 0.7 | 0.62512907 | -0.47029891 | -0.29399752 |
| 48.86 | 0.8 | 0.86026969 | -0.35742717 | -0.30748376 |
| 50.71 | 1.0 | 0.94038206 | -0.13168370 | -0.12383298 |
| 49.43 | 1.1 | 0.88495296 | -0.01881196 | -0.01664770 |
| 48.14 | 1.3 | 0.82909082 | 0.20693152 | 0.17156503 |
| 53.29 | 1.4 | 1.05210633 | 0.31980326 | 0.33646704 |
| 65.14 | 1.6 | 1.56525852 | 0.54554674 | 0.85392168 |
| 65.86 | 1.9 | 1.59643738 | 0.88416196 | 1.41150920 |
| 63.43 | 2.0 | 1.49120871 | 0.99703370 | 1.48678533 |
| 43.14 | 2.1 | 0.61257091 | 1.10990544 | 0.67989579 |
| 31.14 | 2.2 | 0.09292313 | 1.22277718 | 0.11362428 |
| 29.43 | 2.3 | 0.01887332 | 1.33564892 | 0.02520813 |
| 25.71 | 2.3 | -0.14221749 | 1.33564892 | -0.18995264 |
| 19.14 | 2.4 | -0.42672466 | 1.44852065 | -0.61811948 |
I’ve filtered to only the rows where we don’t have NAs, and then found the means and _SD_s, from which we can find the z-scores and the product of them. Scroll through the data and take a look.
If we then take the sum of those products (i.e., add up everything in the final column), we get 11.62. If we take that divided by \(N-1\) (which is the number of rows for which we have data, here 24, with one subtracted from it, therefore 23), we get \(\frac{11.62}{23}=0.505\). That’s exactly what we got in Jamovi.
We can test how likely it is that we’d find an answer like that, too. Your textbook explains that the way we test an r-value is by using this equation for t: \(t=\frac{(r)\sqrt{N-2}}{\sqrt{1-r^2}}\). That \(N-2\) is where the degrees of freedom comes from for this test. We can calculate that t. We know that \(r=0.505\) and \(N=24\). So if we plug those in, \(t=\frac{(0.505)\sqrt{24-2}}{\sqrt{1-0.505^2}}\) and therefore \(t=\frac{(0.505)\sqrt{22}}{\sqrt{1-0.255}}=\frac{2.369}{0.863}=2.746\). You can look in a t-table (where \(t_{crit}(22)=2.07\) for \(\alpha=.05\)), but suffice to say that you can reject the null hypothesis that this correlation is equal to 0, just as was indicated in the Jamovi test. So we can write:
The two indices were significantly associated, \(r(22)=.505,p<.05\). When searches for Ebola increased on the index, the likelihood of voting for Republican candidates also increased.
Remember that we don’t usually report the t-value; we just report the df as \(N-2\), the \(r\), and whether p is less than .05.
Regression
What about a regression? In a correlation, we can put the variables in either order – they’re irrelevant. But in a regression, we’re talking about statistical prediction: one coming before the other. Sometimes that’s not wholly obvious. Fortunately, in this case, the order seems clear: we’re asking whether the Ebola cases in the U.S. changed voting habits, and therefore the Ebola index is the independent variable (IV) and the voting index the dependent variable (DV).
In Jamovi, you’ll go to Analyses, click on Regression, and then click on Linear Regression. Your DV goes in the line for the dependent variable; your IV is the “covariate”. (You can add categorical variables in more complicated regression; those go under “Factors”.) Again, I haven’t given you the data, yet.
| R | R2 |
|---|---|
| 0.505 | 0.255 |
| Predictor | Estimate | SE | t | p |
|---|---|---|---|---|
| (Intercept) | 0.555 | 0.260 | 2.137 | 0.044 |
| Ebola.Search.Volume.Index | 0.019 | 0.007 | 2.747 | 0.012 |
What do you make of this? Refer to the notes/slides from class to try to draw conclusions (if needed), or just puzzle through it; then discuss with a classmate. Finally, read my conclusions:
What do you conclude from the regression results?
The line under the intercept is our predictor: the results show that voter intentions (the dependent variable) are significantly predicted by Ebola searches (Ebola.Search.Volume.Index)—the p-value is the same, in fact, as the one we found above with the correlation. Not a surprise, I hope, since these are mathematically very similar. You may also note that the t-value for Ebola.Search.Volume.Index is the same as the t-value that we calculated earlier for the test on r; this makes sense, too!
We mostly ignore the intercept for this kind of analysis. It doesn’t matter (much) if it’s statistically-significant, or not.
That \(R^2\) at the top of the output is what we call “R-squared”—it is literally the correlation (above), squared. In a regression, we call \(R^2\) “variance explained”. That’s because it’s how much of the variability in our dependent variable is explained by the independent variable.
Depending on what you’re interested in, you’d either report the \(R^2\) and the p-value for the whole model (here, \(p=.01177\) or just \(p<.05\)), or the specific Estimate and p-value for the term of interest. (Or both.) You might say:
The regression model found a significant relationship between voter intention index and Ebola search index, \(R^2=.26,p<.05\). The Ebola search volume index had \(b=0.02,t(22)=2.75,p<.05\) in predicting voter intentions.
Another thing that the regression summary gives you is an “Estimate” of the coefficients, which is a piece from the linear equation you might remember from high school geometry. Remember that old idea of \(y=mx+b\), where m was the slope and b was the intercept? The same thing is true here, too. However, our names for the terms are different. We write our equation as \(y=b_1x+b_0\), where each number we’re figuring out is a subscripted coefficient called b. Thus the \(b_1\) is the slope and the \(b_0\) is the intercept.
If we look at the “Estimate” column in the summary(model) above, you’ll see that it gives us an estimate for the Intercept—\(b_0\)—and for Ebola.Search.Volume.Index—the slope or \(b_1\). Remember how we plotted the points against one another? Technically, if we manually added the intercept and slope from those \(b_0\) and \(b_1\), we’d get the same line we got above:
Now try it yourself
Importing data
As discussed in the section above, we’re using data from Beall, Hofer, & Shaller (2016).
Beall, A. T., Hofer, M. K., & Shaller, M. (2016). Infections and elections: Did an Ebola outbreak influence the 2014 U.S. federal elections (and if so, how)? Psychological Science, 27, 595-605. https://doi.org/10.1177/0956797616628861
Make sure you read the description of the study in the tutorial—it’s important for thinking about what we’re doing in these exercises.
In the tutorial, I showed you a “cleaned-up” version of the data. But let’s actually use the raw data here: it’s on Brightspace and here. Download it and open it in Jamovi.
Today’s task
To start: Clean the data by removing the two lines at the very top for which there are NAs even in the Date and Month column. You should now have 65 rows.
You may want to practice by running the correlation and regression analyses we did above, for the association between Ebola search volume index and voter intention index. Do you get the same results we did above? They may look slightly different, but they should be (rounded) the same.
The authors report that “Across all days in the data set, [the Ebola-search-volume index] was very highly correlated with an index—computed from LexisNexis data—of the mean number of daily news stories about Ebola during the preceding week, \(r = .83, p < .001\).”
Calculate this correlation yourself using Jamovi’s Correlation Matrix. (You’ll use the columns
Ebola.Search.Volume.IndexandLexisNexisNewsVolumeWeek) Then, briefly report the correlation as we discussed above, including reporting if it’s significant. This is #1.Plot that relationship using the scatr plugin, as we did in lab 3. (That’s a link; feel free to remind yourself. It’s the third question.) I recommend putting
Ebola.Search.Volume.Indexas the x-axis. Put on a linear regression line. Add the standard error. Copy this plot into your answer document as #2.Run a regression on the same relationship (“Linear Regression” menu). Consider
LexisNexisNewsVolumeWeekas the covariate andEbola.Search.Volume.Indexas the DV. Report your results as #3. Also report what parallels exist between the numbers from this regression and the correlation.
Filter to only use the scores from the two-week period including the last week of September and the first week of October. You could look at the Month and Date columns… but the third column might be more helpful. (I recommend using that one.)
- With the filtered data, re-run the correlation analyses for the association between Ebola search volume index (
Ebola.Search.Volume.Index) and voter intention index (Voter.Intention.Index), the two columns from the beginning of lab. Is the correlation higher or lower than what we already found (i.e., in the unfiltered data)? Repeat the analysis as a regression, predicting voter intentions from search indices. Report all of your results, and your conclusion as #4. Also include a scatterplot of the results.
That’s what correlations and regressions look like in Jamovi, in their simple form. Make sure you understand what we’re doing here, check in with your classmates, and then you’re done. Don’t forget to submit your write-up on Brightspace.
Reuse
Citation
BibTeX citation:
@online{dainer-best2023,
author = {Dainer-Best, Justin},
title = {Correlation and {Regression} {(Lab} 9)},
date = {2023-11-09},
url = {https://faculty.bard.edu/jdainerbest/stats/labs//posts/09-correlation-regression},
langid = {en}
}
For attribution, please cite this work as:
Dainer-Best, Justin. 2023. “Correlation and Regression (Lab
9).” November 9, 2023. https://faculty.bard.edu/jdainerbest/stats/labs//posts/09-correlation-regression.