Sage is a very powerful free open source computer program for mathematical calculations. It is useful in calculus, linear algebra, differential equations, and much more; it does numerical and symbolic calculations, and both 2D and 3D graphics.
Sage, which is a cloud-based program, can be accessed from any computer via a web browser. There are two ways to use Sage: the quick version and the full version.
To use the quick version of Sage, which is good for simple computations and which does not require setting up an account, simply go to the website
To use the full version of Sage, you first need to set up a free account. To set up an account and log in, go to the website
Although you don't need any prior knowledge of computer programming to use Sage, one of the advantages of Sage is that it is based upon the Python programming language, which is the language taught in Bard's Object Orient Programming course (CMSC 141 or CMSC 143).
There are a number of sources on the web for learning for Sage. Some particularly useful ones are the following.
This textbook by Gregory Bard, which is published by the American Mathematical Society, is available in PDF format for free at the author's website. This website has links for the textbook and for other useful Sage resources.
These two videos by Gregory Bard, which use the convenient SageMathCell server, provide a nice introduction to some basic Sage commands.
These quick reference have very convenient summaries of basic Sage commands. The first quick reference has basic Sage commands, and the other quick references are for specific topics.
Each of the following interactive Sage demonstrations can be accessed via its own webpage. Brief instructions are given for each demonstration.
These interactive demonstrations can be used without any knowledge of Sage.
If you find any errors or problems with these demonstrations, please let me know.
Calculus Demonstrations
Linear Algebra Demonstrations
Probability and Statistics Demonstrations
Various basic Sage commands are demonstrated below. Each command, or group of commands, appears in a Sage Cell. To evaluate the commands, click on the Evaluate button below the cell. The result of doing the operation will appear in a new box below the Evaluate button.
If there is an error in the commands in a Sage Cell, a notice of the error will appear in the box below the Evaluate button.
The commands in any of these Sage Cells can be modified as many times as desired, and then evaluated each time.
Sage commands are meant to resemble normal mathematical notation as much as possible. However, as with any computer programming language, it is important to write Sage commands very precisely.
Here are a few basic rules for writing commands in Sage.
The operations of addition, subtraction, multiplication and division are written \(+\), \(-\), \(*\) and \(\div\). Do not neglect to write \(*\) every time you do multiplication.
Sage follows the usual order of operations.
Sage works in fractions if that is the input, and in decimals if that is the input.
Use the following modification to convert an answer in fractions to decimals.

Sage has built in functions that are written just as you would expect, for example \(\sin (x)\).
You can define, and evaluate, functions just as you normally would.
A function can have more than one variable.
Note: The letter \(x\) is pre-defined as a variable; any other letter to be used as a constant or variable needs to be defined at the start of the commands, as follows.
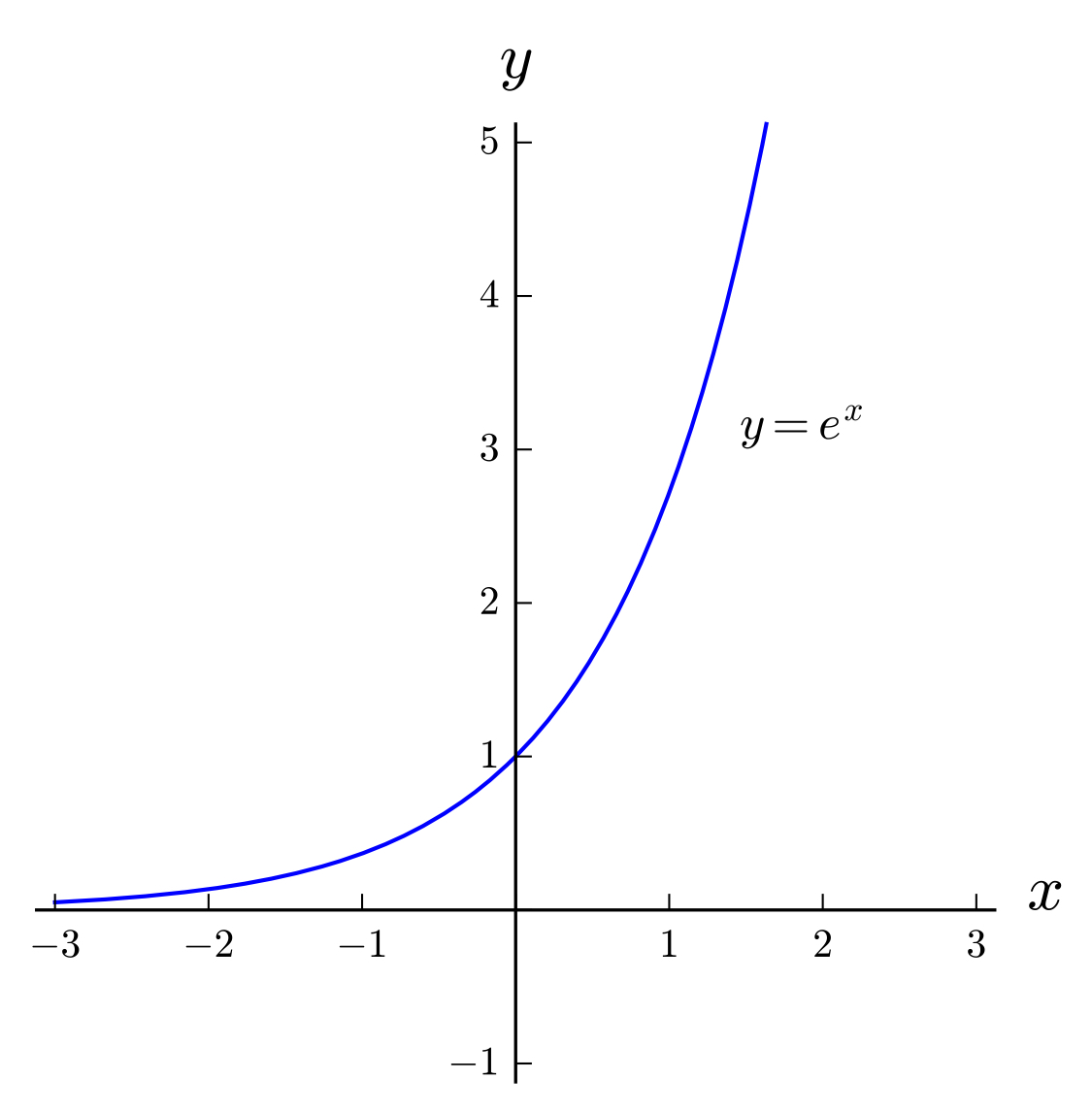
In the command for plotting a function of one variable, the domain of \(x\) must be specified.
If you want the aspect ratio of the image to be \(1\), you can specify that.
Plotting Two Functions at Once
When a function has more than one variable, the variables must be defined.
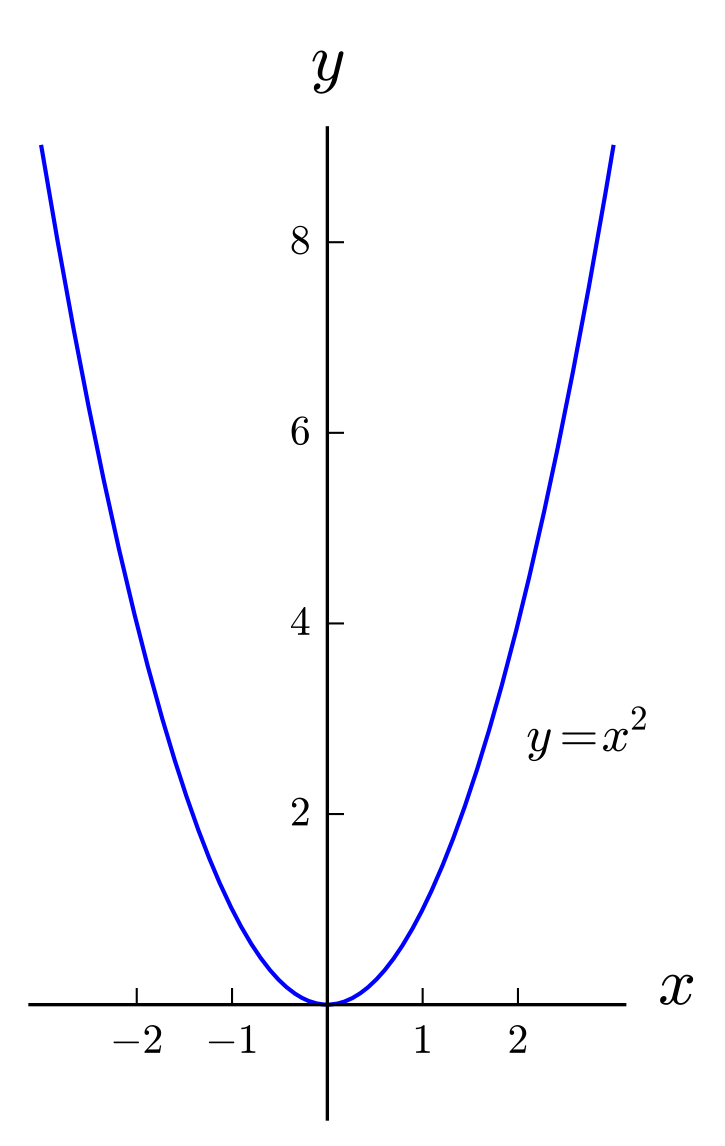
In the command for plotting a function of two variables, the domain of \(x\) and \(y\) must be specified.
The image of a function of two variables can be slow to load.
The image of a function of two variables can be rotated by clicking and holding it with the mouse and then moving it.
A regular derivative is straightforward to compute.
When finding a partial derivative of a function of more than one variable, it is important to state the name of the variable with respect to which the partial derivative is taken.
When finding the indefinite integral of a function, it is important to state the name of the variable after stating the function.
When you find an indefinite integral, note that Sage does not give the \(+ C\), though of course you need to add that when you write the solution.
The command for finding a definite integral is the same as the command for an indefinite integral, except that the limits of integration are added.
Use the following modification to find a definite integral with decimal answer
A list is similar to a set, though in a list the elements have the given order.
Single elements of a list can be called using the index for the element.
Note: In a list in Sage, the first element has index \(0\), the second element index \(1\), etc., rather than the more common method of starting the indices at \(1\).)
Lists can be generated very similarly to the way sets are defined. Note that the variable used for generating the list exists only inside the definition (similarly to the variable used in defining a set), and therefore does not need to be defined previously.
Solving an equation is simple, as long as two issues are noted.
Note: The equals sign in the equation is typed with a double equals.
Note: The unknown being solved for must be specified.
An equation with more than one unknown can be solved for any one of the unknowns in terms of the others.
Systems of equations can be solved as follows.
When using the solve command in Sage, the set of solutions is given as a list containing the variable and solutions. To extract single numerical values of the solutions, use the following command.
Note: As with all lists in Sage, the first element has index \(0\), the second element index \(1\), etc., rather than the more common method of starting the indices at \(1\).)
Sage can handle matrices very easily, though there is one issue to note.
Note: When you define a matrix in Sage, it is important to state what set of numbers is being used: QQ (rational numbers), or RR (real numbers) or CC (complex numbers).
Matrices can be added, subtracted and multiplied using the same method as adding, subtracting and multiplying numbers.
Determinants are easy to compute.
Eigenvalues are easy to compute. The letter \(I\) in a solution indicates the imaginary number standardly written \(i\).
It is simple to make an interactive program in Sage. In the following example, which is the graph of the function \(y = A\sin(Bx + C)\), you to change the values of \(A\), \(B\) and \(C\), as well as the intervals in the \(x\)-axis and \(y\)-axis that is visible.
Interactive programs in Sage use a variety of tools such as sliders buttons, selector buttons, input boxes and range sliders, all of which are shown in the following example.
When you use the interact command in Sage, it is crucial to indent the various parts of the program as shown (other than the fact that some lines have been broken in two in order to fit in a small box).
Ethan Bloch
Professor of Mathematics
Bard College
Office Hours: