Research

I am interested in the elusive harmony between gravity and quantum mechanics. Is time discrete? Is space made of fundamental grains and, if so, how do they mesh to create the smooth continuum we experience and measure? Can black holes truly outlive everything else in the universe? I develop simple, but robust models to address these questions drawing heavily from the classical and geometrical foundations of general relativity. For example, I have fruitfully used these ideas to produce a new and independent road to the quantization of space that is in excellent agreement with that found in loop gravity (see [1]).

I also enjoy mapping exoplanets.

Currently I am investigating an in-principal test of the Bekenstein-Hawking entropy using gravitational waves, the nature of dual boundary theories in discrete gravity, and a new formulation of differential calculus that allows you to flow along momenta. My work on exoplanets has focused on the problem of determining their surface maps from the limited information contained in a light curve. More detailed descriptions of some of my research efforts are given below.

Black hole entropy and singularities

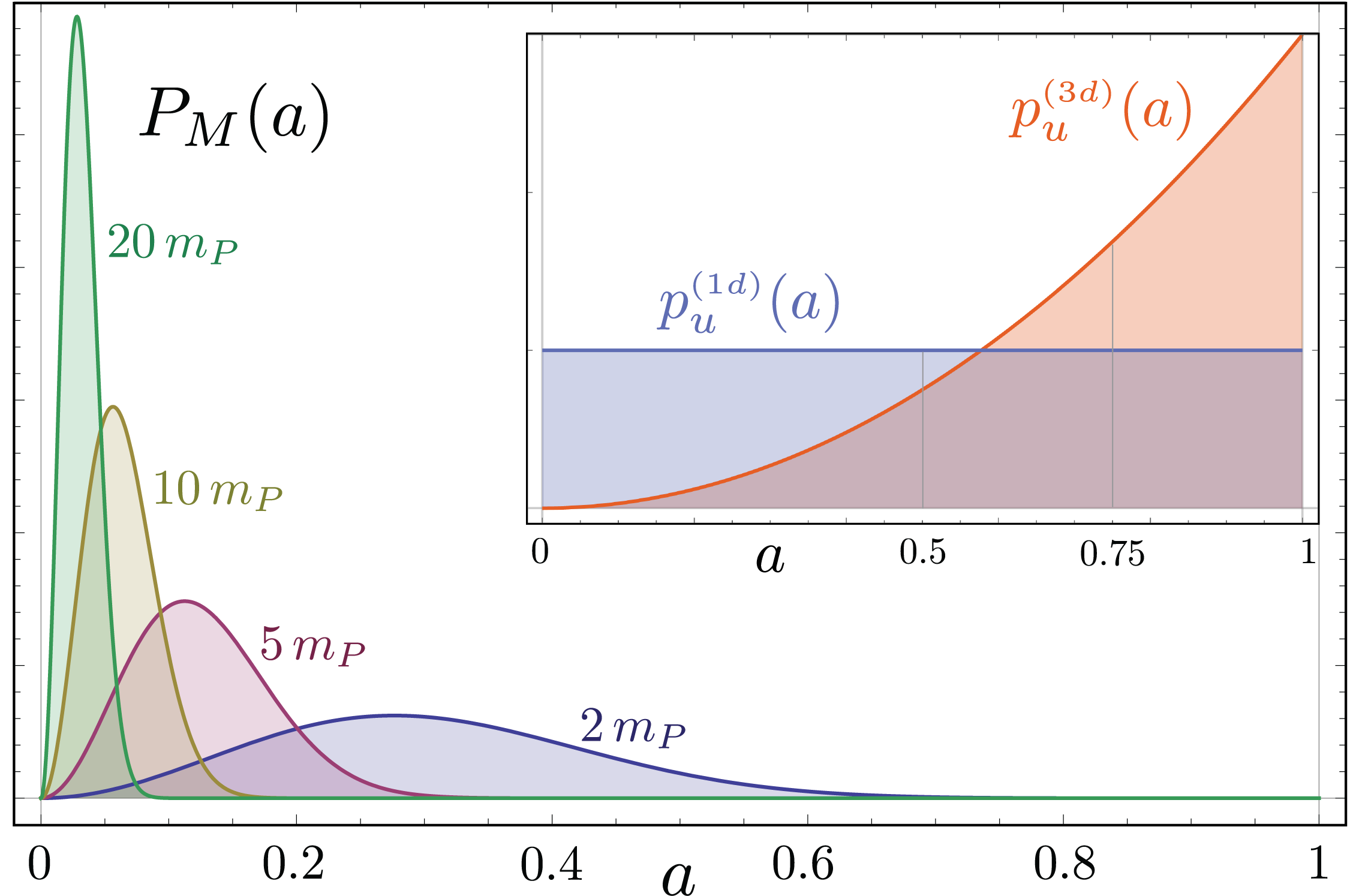Are black holes the simplest macroscopic gravitating objects or the most complex? Classically they are completely characterized by their mass and angular momentum no matter how they are formed, making them incredibly simple. But, they are also supposed to have a gigantic entropy associated to them, the Bekenstein-Hawking entropy. This entropy is proportional to the area of the black hole horizon and is much larger than the entropy of a star of the same mass. Intriguingly, this entropy is such a robust feature of black holes that it is often used as a viability test for quantum theories of gravity. In recent work I have been investigating the quantum nature of the inner singularities of black holes and looking into how we can observationally test the remarkably robust Bekenstein-Hawking entropy.

Black hole evaporation

Since the discovery of Hawking radiation physicists have searched for a consistent picture of the full life cycle of a black hole. Quantum mechanics allows particles to escape the vicinity of the black hole as Hawking radiation, but it is difficult to understand how these particles can carry away all the information stored in a black hole. Carlo Rovelli and I have recently proposed an alternative scenario; we see the formation and dissolution of a black hole as a super slow motion crunch and explosion—a quantum mechanically driven bounce from a black to a white hole. This gives a radically different perspective on the black hole information puzzle. Nature News article on these ideas. Academic Minute radio spot.

The cosmological constant in quantum gravity

"Even a tiny cosmological constant casts a long shadow."

—Abhay Ashtekar

The universe is expanding faster and faster. This empirical observation is included in Einstein's theory of gravity as the cosmological constant. The measured value of this constant is Λ = 2.90×10^-122 in Planck units. Despite its remarkably small value, the cosmological constant has a huge effect on our universe. It changes the curvature, wrapping the universe up like a ball, and causes it to expand at an ever faster rate. It also has a big impact on quantum gravity.

Researchers in both loops and strings have struggled to include a positive cosmological contant in their theories. We have proposed a new model that does just this by combining tools from both fields with the mathematics of knots.

Chaos in a grain of space

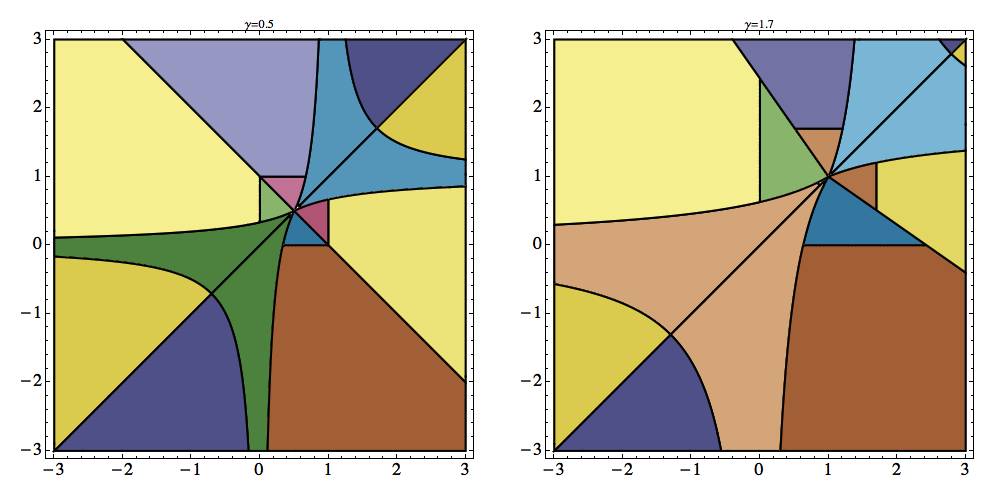
In quantum gravity space is expected to have a discrete, quantum structure and to be built up out of many atomic grains of space. These grains can be modeled with the simplest 3D geometry you first encounter in mathematics, polyhedra. The most basic polyhedron is the tetrahedron, a pyramid with a triangular base. Myself and others have studied this most basic building block extensively. But, only recently have we turned to more complex grains of space, such as the pentahedron.

Pentahedra have a wonderfully rich dynamics. For example it is possible to fix the volume and face areas of a pentahedron and still deform it in such a way as to change which faces are neighbors. Each of the panes in the stain-glass figure at right shows a region of the phase diagram of a pentahedron with a different adjacency of its faces. Study of these regions has led to the conclusion that the dynamics of the volume of a pentahedron is chaotic. This work has opened a new window onto quantum chaos in quantum gravity.

Mapping Exoplanets

There is a wonderful inverse problem in the emerging field of planets outside our solar system: Given only the total light coming from an extrasolar planetary system how can we infer properties of the surface map of a planet contained in the system? I've worked on this problem with the remarkable Nicolas Cowan and several teams of undergraduate students.